Формула Бернуллі
Нехай проводиться п незалежних випробувань, причому ймовірність появи події А в кожному випробуванні одна й та сама, тобто не залежить від її появи в інших випробуваннях. Таку серію повторних незалежних випробувань називають схемою Бернуллі. Прикладом повторних незалежних випробувань є підкидання монети певну кількість разів, стрільба по мішені тощо.
Нехай випадкова подія А може відбутися в кожному випробуванні з однаковою ймовірністю Р(A) = р або не відбутися з імовірністю q = 1 – p. Імовірність того, що при n випробуваннях подія А відбудеться m разів, визначається за формулою Бернуллі:
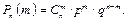
| (8) |
Імовірність появи події А в n випробуваннях m разів, де число m перебуває між числами k1 і k2, 0 £ k1 £ k2 £ n, знаходиться за формулою
Рn(k1 £ m £ k2) = Рn(k1) + Рn(k1 + 1) + ... + Рn(k2).
Імовірність появи події А в n випробуваннях хоча б один раз
Рn(1 £ m £ n) = 1 – qn.
Найімовірніша кількість m0 появи події А в n випробуваннях визначається з нерівностей
n · p – q £ m0 £ n · p + p.
Якщо ймовірність появи події А в кожному випробуванні дорівнює р, то кількість n випробувань, які необхідно здійснити, щоб з ймовірністю Р можна було стверджувати, що подія А відбудеться хоча б один раз, обчислюється за формулою
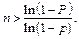
Приклад 8. Прилад складено з 10 блоків, надійність кожного з яких 0,8. Блоки можуть виходити з ладу незалежно один від одного. Знайти ймовірність того, що:
а) відмовлять два блоки;
б) відмовить хоча б один блок;
в) відмовлять не менше двох блоків.
Знайти найімовірнішу кількість блоків, що вийдуть з ладу.
Розв’язання. Позначимо подію А= {відмова блока}. Тоді
Р(A) = р = 1 – 0,8 = 0,2.
Тому q = 0,8. За умовою задачі n = 10. Застосувавши формулу Бернуллі (8) та наслідки з неї, матимемо:
а) 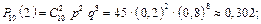
б) 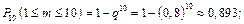
в) 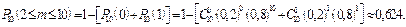
Найімовірнішу кількість блоків, що вийдуть з ладу, знайдемо з нерівностей
n · p – q £ m0 £ n · p + p,
тобто
10 · 0,2 – 0,8 £ m0 £ 10 · 0,2 + 0,2.
Отже,
m0 = 2. ·
Дата добавления: 2015-08-26; просмотров: 2260;
