Формула повної ймовірності. Формула Байєса
Якщо випадкова подія А може відбутися лише сумісно з однією із несумісних між собою подій В1, В2, ..., Вn, що утворюють повну групу, то ймовірність появи події А обчислюється за формулою повної ймовірності
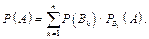
| (6) |
В умовах теореми невідомо, з якою із несумісних подій В1, В2, ..., Вn відбудеться подія А. Тому появу кожної з цих подій можна вважати гіпотезою, а Р(Вk) — імовірністю k-ї гіпотези.
Якщо в результаті проведеного випробування відбулася подія А, то умовна ймовірність РA(Вk) може не дорівнювати Р(Вk). Щоб отримати умовну ймовірність, використовують формулу Байєса:
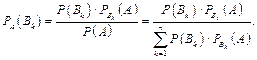
| (7) |
Приклад 7. Деталі, виготовлені цехом заводу, потрапляють для перевірки їхньої стандартності до одного з двох контролерів. Імовірність того, що деталь потрапить до першого контролера, дорівнює 0,6, до другого — 0,4. Імовірність того, що придатна деталь буде визнана стандартною першим контролером, дорівнює 0,94, другим — 0,98. Придатна деталь при перевірці визнана стандартною. Знайти ймовірність того, що деталь перевіряв:
• перший контролер;
• другий контролер.
Розв’язання. Позначимо такі події:
А = {придатна деталь визнана стандартною};
В1 = {деталь перевіряв перший контролер};
В2 = {деталь перевіряв другий контролер}.
Тоді згідно з умовою задачі
P(B1) = 0,6; P(B2) = 0,4; 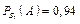 ;
; 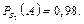
Згідно з формулою Байєса (7) маємо
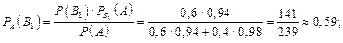
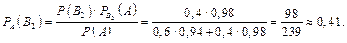 ·
·
Дата добавления: 2015-08-26; просмотров: 1974;
