Использование преобразований Фурье, Лапласа и Карсона — Хевисайда

Как известно, периодическая функция времени, подчиняющаяся условиям Дирихле, может быть разложена в ряд Фурье:

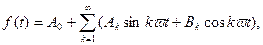
где k — порядок гармоники, а 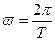— основная круговая частота.

Этот ряд может быть представлен также в комплексной форме:

,

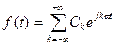где комплексный коэффициент 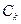определяется выражением

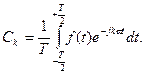
Таким образом, периодическая функция времени может быть представлена в виде совокупности дискретных гармоник с интервалом по частоте между соседними гармониками, равным основной частоте ω.

Непериодическая функция времени может рассматриваться как периодическая с периодом, стремящимся к бесконечности. В этом случае вместо приведенных формул получаются два интегральных уравнения Фурье, связывающих оригинал, т. е. функцию времени f(t), и ее частотное изображение F(jω), которое называется также преобразованием Фурье:

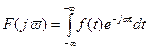, (7.15)

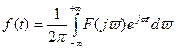(7.16)

В отличие от разложения в ряд Фурье здесь получается разложение в непрерывный спектр частот с интервалом по частоте между соседними гармониками, равным бесконечно малой величине .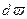

Недостатком интеграла Фурье является то, что он принадлежит к числу несобственных интегралов и может применяться для так называемых абсолютно интегрируемых функций времени, т. е. для функций времени, удовлетворяющих неравенству

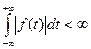
От этого недостатка, свободно преобразование Лапласа, связывающее оригинал и изображение следующими интегральными уравнениями:

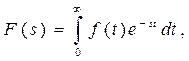(7.17)

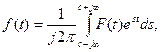(7.18)

причем функция времени должна быть равна нулю (f(t) =0) при t < 0. В отличие от преобразования Фурье здесь изображение функции времени является функцией не частоты, а некоторой комплексной величины s = с + jω. Вещественная часть ее представляет собой так называемую абсциссу абсолютной сходимости, которая выбирается- так, чтобы удовлетворялось неравенство

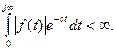
Для большинства функций, с которыми приходится иметь дело в регулировании, абсцисса абсолютной сходимости равна нулю, т. е. с = 0. Поэтому для этих функций преобразование Лапласа переходит в преобразование Фурье, если произвести подстановку s = jω.

Уравнения (7.17) и (7.18) часто записывают в сокращенном виде:

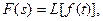
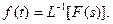(7.19)

Иногда вместо буквы s применяется буква р, т. е. изображение Лапласа записывается в виде F(р), но в этом случае р представляет собой не оператор дифференцирования, а комплексную величину: р = с + jω [1]).

В связи с этим формулы (7.19) и (7.20) могут быть записаны в виде

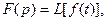
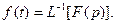(7.20)

В некоторых случаях, особенно в задачах электротехники, используется преобразование Карсона — Хевисайда, которое отличается от преобразования Лапласа дополнительным умножением на величину р:

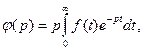(7.21) 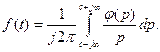(7.22)

Таким образом, между преобразованиями Лапласа и Карсона — Хевисайда существует соотношение

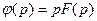. (7.23)

Преобразование Карсона — Хевисайда нашло распространение наряду с' 'преобразованием Лапласа. Это объясняется тем, что исторически первым для решения дифференциальных уравнений был использован так называемый операторный метод Хевисайда, который, по сути дела, использовал|преобра-зования (7.21) и (7.22).

Кроме того, удобство преобразования Карсона — Хевисайда заключается в том, что изображение постоянной величины А, точнее, ступенчатой функции 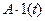, равно самой постоянной величине, что легко доказывается использованием выражения (7.21). Поэтому во многих случаях преобразование Карсона — Хевисайда сливается с операторной записью дифференциальных уравнений.

Основное достоинство преобразований Фурье, Лапласа и Карсона — Хевисайда заключается в том, что операции дифференцирования и интегрирования оригинала заменяются алгебраическими действиями по отношению к изображениям.

В табл. 7.2 приведены основные формулы и свойства изображений Лапласа и Карсона — Хевисайда. Изображение Фурье может быть получено из изображения Лапласа подстановкой р = jω.

Формулы для дифференцирования и интегрирования оригинала даны для случая нулевых начальных условий.

Для ненулевых начальных условий из (7.17) можно получить изображение по Лапласу производной оригинала (s заменено на р):

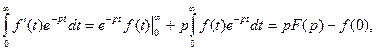(7.24)

где F (р) — изображение самой функции.

Аналогично для второй производной

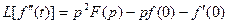(7.25)

и для производной любого порядка

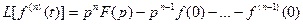. (7.26)

При нулевых начальных условиях

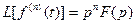(7.27)

или

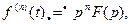(7.28)

т. е. операция дифференцирования оригинала заменяется для изображения умножением на комплексную величину р.

Аналогично для преобразования Карсона — Хевисайда

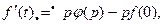(7.29)

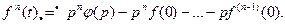(7.30)

При нулевых начальных условиях

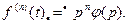
Аналогичным образом можно найти изображение интеграла от функции времени:

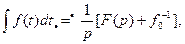(7.31)

где 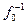представляет собой значение интеграла, находящегося в левой части (7.31), при t= 0:

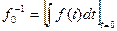
Таблица 7.2

Преобразования Лапласа и Карсона — Хевисайда

Наименование	Оригинал	Изображение Лапласа	Изображение Карсона —Хевисайда
Свойство линейности
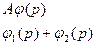
Теорема подобия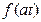
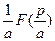
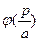
Теорема запаздывания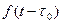
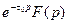
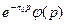
Теорема смещения в комплексной плоскости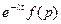
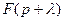
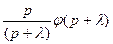
Правило дифференци-рования при нулевых начальных условиях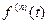
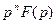
Правило интегрирова-ния при нулевых начальных условиях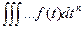
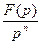
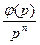
Теорема о конечном значении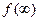
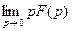
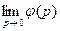
Теорема о начальном значении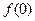
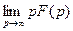
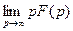
Единичная импульсная функция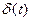
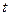
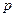
Единичная ступенчатая функция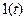
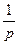
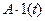
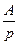
Неединичная ступенчатая функция			A
Степенная функция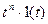
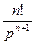
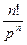
Экспонента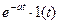
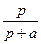
Смещенная экспонента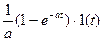
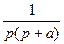
Синусоида
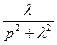
Косинусоида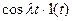
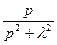
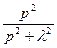
Затухающая синусоида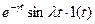
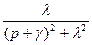
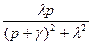
Затухающая косинусоида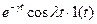

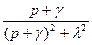
Для нулевых начальных условий выражение (7.31) упрощается:

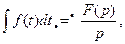
т. е. интегрированию по времени оригинала соответствует деление на изображение на комплексную величину р.

Рассмотрим теперь использование изображений для решения Дифференциального уравнения

(7.32)

на примере преобразования Лапласа.

Перейдем в левой и правой частях (7.32) к изображениям Лапласа. При этом оцёратор дифференцирования 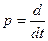в полиномах D(р) и N(р) заменяется аа комплексную величину р = с + jω, а вместо оригиналов x(t) и f(t) появляются их изображения X(р) и F(р). В результате получаем

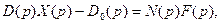
где 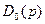обозначает сумму всех членов, содержащих начальные условия.

Отсюда находится изображение искомой величины:

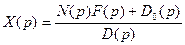(7.33)

Последнее выражение требует некоторых пояснений в связи с различными возможными трактовками понятия начальных условий. Интегральное преобразование Лапласа (7.17), следует, вообще говоря, записать в более строгом виде (при замене s на р):

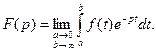(7.34)

Это дает возможность введения двух несколько отличающихся понятий преобразования Лапласа (и соответственно преобразования Карсона — Хевисайда).

1. Преобразование Лапласа по начальным условиям справа. Если в выражении (7.34) нижний предел интегрирования стремится к нулю, оставаясь положительным (а > 0), то в изображении производной (7.26) следует брать начальные условия при t = + 0, т. е. для момента времени, который будет сразу после приложения к системе внешних воздействий. В этом случае

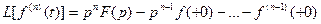
Для использования последней формулы необходимо знание начальных условий справа, что оказывается не всегда удобным и требует расчета по формулам § 7.З. Заметим, что даже в тех случаях, когда до приложения воздействия система находилась в покое, начальные условия справа могут быть ненулевыми и полином 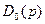, как правило, отличен от нуля.

Кроме того, если рассматриваемая функция времени f(t) имеет при t = 0 особенности типа δ-функции, то это обстоятельство не будет учтено в найденном изображении. Так, например, изображение самой δ-функции и ее производных оказывается при этом равным нулю:

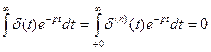
2. Преобразование Лапласа по начальным условиям слева. Если в формуле (7.34) нижний предел интегрирования стремится к нулю, оставаясь отрицательным (а <0), то в выражении для изображения производной (7.26) следует брать начальные условия при t = — 0, т. е. для момента времени, который будет непосредственно предшествовать моменту приложения воздействия. Такие начальные условия называются также предначалъными. В этом случав

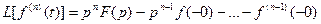
Расчет получается более простым, так как предначальные условия должны быть известны всегда и никаких дополнительных операций здесь не требуется. В частном случае, когда до приложения воздействия система находилась в покое, предначальные условия нулевые и выражение (7.33) приобретает вид

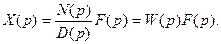
Только это выражение и позволяет строго сформулировать понятие передаточной функции W(р) как отношение изображений входной и выходной величин при нулевых предначальных условиях.

Кроме того, преобразование Лапласа в случае, когда нижний предел интегрирования стремится к нулю, оставаясь отрицательным (а < 0), позволяет учитывать наличие в рассматриваемой функции при t = 0 особенностей типа δ-функции. Так, например, изображение единичной б-функции оказывается равным единице:

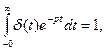
а изображение ее производной n-го порядка

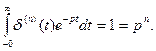
Влияние особенностей f(t) и ее первых т производных, где m — порядок полинома N(р), на изображение N(р)f(t) в этом случае и проявляется в виде автоматического учета начальных условий, которые будут иметь место справа (при t= +0) в самом изображении N(р)F(р) без введения дополнительного члена 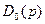при нулевых предначальных условиях или без его изменения при ненулевых предначальных условиях. В связи с этим δ -функция иногда называется также функцией начальных условий.

В дальнейшем изложении под преобразованием Лапласа будет пониматься именно этот случай (а < 0).

Зная изображение искомой величины X(р) в виде (7.33) или (7.35), можно найти оригинал х(t). Это и будет решением исходного дифференциального уравнения (7.32).

Для отыскания оригинала х(t) по его изображению X(р) можно пользоваться таблицами изображений и существующими теоремами, в частности теоремой разложения, которая устанавливает следующее. Если изображение Лапласа имеет вид отношения двух многочленов

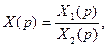(7.36)

то при отсутствии нулевых корней знаменателя

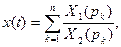(7.37)

где 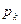— некратные корни знаменателя (7.36).

Если знаменатель изображения Лапласа (7.36) имеет нулевой' корень (p₀ = 0), то изображение надо представить в виде

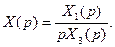(7.38)

Тогда оригинал может быть найден по формуле

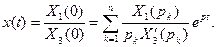(7.39)

Аналогичным образом теорема разложения может быть записана и для преобразований Карсона — Хевисайда. Так, например, если изображение искомой величины может быть представлено в .виде отношения двух полиномов

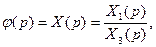(7.40)

то при отсутствии нулевых и кратных корней знаменателя оригинал будет определяться выражением

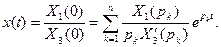(7.41)

Это выражение полностью совпадает с формулой (7.39), так как изображения Лапласа (7.38) и Карсона — Хевисайда (7.40) отличаются на множитель р.

Использование изображений часто называют также операторным методом, хотя в действительности операторному методу, разработанному Хеви-сайдом, оказывается полностью аналогичным использование только преобразований Карсона — Хевисайда (7.21) и (7.22).

Метод использования изображений обладает тем преимуществом, что в нем полностью сохраняется лишь одна операция — вычисление корней характеристического уравнения (знаменателя изображения). Что касается определения произвольных постоянных интегрирования, то эта операция отпадает, потому что начальные условия автоматически учитываются в процессе решения с самого начала (при нахождении изображения искомой величины). Поэтому этот метод оказывается удобным и его часто применяют в задачах теории регулирования.

Практически важной для отыскания оригинала решения является еще теорема свертывания. Она гласит следующее. Если изображение представляет собой произведение

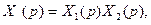(7.42)

то оригинал выражается формулой

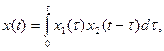(7.43)

где 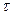представляет собой вспомогательное время интегрирования.

В частности, пусть для некоторой системы с передаточной функцией W(р) известна реакция на единичную импульсную функцию , представляющую собой функцию веса и связанную с W(р) преобразованием Лапласа

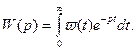
Если на вход этой системы поступает некоторая функция времени f(t), изображение которой F(р), то изображение выходной величины будет

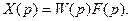
Тогда функция времени на выходе может быть найдена по интегралу свертывания (7.43), который совпадает с интегралом Дюамеля (4.9):

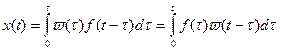(7.44)

Если входная функция определена только для положительного времени {прикладывается на вход в момент времени t = 0), то функция 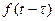отлична от нуля только при 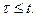В этом случае верхний предел интеграла в формуле (7.44) может быть заменен на бесконечность и она приобретает вид

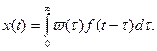(7.44)

5. ВЫЧИСЛЕНИЕ УСТАНОВИВШЕЙСЯ ОШИБКИ АВТОМАТИЧЕСКОЙ СИСТЕМЫ

Теория автоматического управления рассматривает автоматические системы в информационном плане, т. е. с точки зрения передачи и преобразования сигна­лов. Поэтому вполне естественно возникает вопрос: с какой точностью переда­ются эти сигналы? В частности, нас будет интересовать точность воспроизве­дения задающего воздействия, а именно: с какой степенью точности выполня­ется основное условие х_вых(t) =х_вх(t). Кроме того, необходимо определить ошибки, вызванные возмущением f (t). Ошибка системы по задающему воздей­ствию:

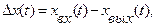
а по возмущению:

т. е. ошибка системы от возмущения численно равна изменению регулируемой величины под влиянием этого возмущения (при отсутствии задающего воздей­ствия).

Ввиду наличия переходных процессов текущее значение ошибки 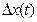резко меняется и не может служить мерой точности автоматических систем. По этому условились точность автоматических систем оценивать величиной установившейся ошибки, которая имеет место в устойчивой системе после заверше­ния переходного процесса.

Итак, нам необходимо установить, во-первых, как вычисляются установив­шиеся ошибки и, во-вторых, какие факторы влияют на эти ошибки. Обе задачи будем решать параллельно. Предварительно отметим, что установившаяся ошибка вычисляется для значения времени , т. е.

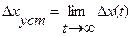
Величину установившейся ошибки можно найти из дифференциального уравнения системы, однако ее значительно удобнее вычислять при помощи передаточной функции ошибки 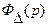. Действительно, по определению,

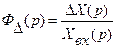
Следовательно,

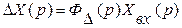
Данная формула позволяет найти изображение ошибки. Для того чтобы найти ошибку как функцию времени, необходимо сделать обратное преобразование Лапласа:

,

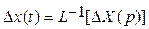откуда можно определить установившуюся ошибку, положив .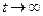

Однако данный способ вычисления 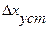не рационален, поскольку мы вна­чале находим ошибку как функцию времени и затем вычисляем ее значение для одной лишь точки . А нельзя ли сразу по известному изображению 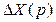найти 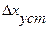, минуя промежуточный этап определения 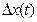? Оказывае­тся, можно и притом весьма просто! Для этого применим теорему операцион­ного исчисления о конечном значении функции. Эта теорема говорит о том, что если известно изображение 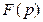функции 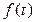, то конечное значение оригинала 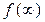можно вычислить по формуле

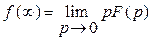
Применяя эту формулу для решения нашей задачи, получаем

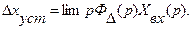(132)

Формула (132) позволяет вычислить установившуюся ошибку по задающе­му воздействию . Для определения установившейся ошибки от возмуще­ния f (t) надо воспользоваться зависимостью

, (133)

где 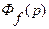— передаточная функция по возмущению.

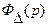Таким образом, из формул (132) и (133) следует, что точность автоматических систем зависит, во-первых, от внешнего воздействия или f (t) и, во-вторых, от свойств автоматической системы, отображаемых передаточной Функцией или .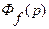

В общем случае как задающее, так и возмущающее воздействие является сложной функцией времени, при которой вычисление ошибок значительно усложняется и даже становится невозможным. Как же выйти из этого поло­жения? Заменим реальные воздействия типовыми, т. е. достаточно простыми для того, чтобы можно было определить ошибки. Но какое мы имеем право слож­ные реальные воздействия заменять простыми? Во-первых, внешние воздейст­вия у некоторых систем близки к типовым, и, во-вторых, при проектировании автоматических систем необходимо сравнить между собой различные варианты и выбрать лучший.

Это удобно сделать при типовых воздействиях, в каче­стве которых применяют ступенчатую 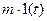, линейную 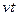и квадратичную 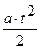функции. Можно применять и более сложные воздействия.

Все эти воздействия просто выражаются при помощи формул; их значения можно точно вычислить для любого момента времени, ввиду чего они называю­тся детерминированными, или регулярными.

Однако внешние воздействия часто являются случайными функциями вре­мени. Тогда для оценки точности автоматических систем применяют статисти­ческие методы, что мы рассматривать не будем.

6. ОШИБКИ ОТ ЗАДАЮЩИХ ВОЗДЕЙСТВИЙ

Получим формулу для вычисления ошибки от задающего воздействия. Учиты­вая равенство (132), а также выражение для передаточной функции ошибки

,

получим

, (134)

где W (p) — передаточная функция разомкнутой системы.

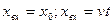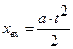При вычислении ошибок по формуле (134) необходимо иметь в виду, что изо­бражение по Лапласу типовых воздействий для и соответственно равны:

;

;

.

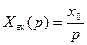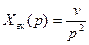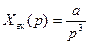Кроме того, для статистических систем 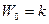, а для астатических сис­тем 1-го и 2-го порядков примем соответственно W (p) = W* (р) и W (р)= 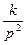W* (p), при этом W* (0) =1, где k — коэффициент передачи разомкну­той системы; W* (р) — передаточная функция без учета интегрирующих звень­ев и коэффициента передачи.

Рассмотрим теперь ошибки некоторых автоматических систем. Как видно из табл. 3, статические системы при ступенчатом воздействии имеют установившу­юся ошибку

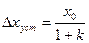, (135)

которая называется статической, или ошибкой по положению. Она пропорцио­нальна величине задающего воздействия и уменьшается с увеличением коэффи­циента передачи разомкнутой системы k. При изменяющихся во времени воз­действиях ошибка непрерывно возрастает, ввиду чего эти системы в качестве следящих применять нецелесообразно. Наличие статической ошибки являет­ся характерным свойством статических систем.

Таблица 3: