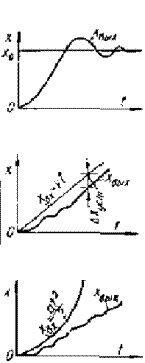
Реакции автоматических систем на типовые задающие воздействия и установившиеся ошибки
| Статическая система (v = 0) | Астатическая система | ||||
| v = 1 | v = 2 | ||||
| Установив-шаяся ошибка | Реакция системы | Установив-шаяся ошибка | Реакция системы | Установив-шаяся ошибка | Реакция системы |
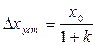
| 
| 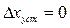
| 
| 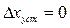
| 
|
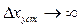
| 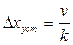
| 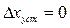
| |||
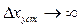
| 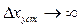
| 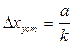
|
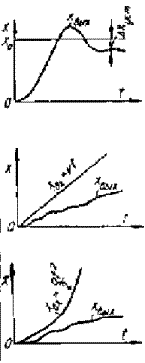
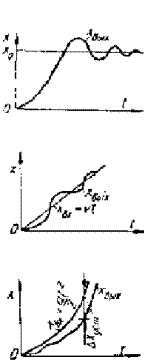
Астатические системы 1-го порядка принципиально точно отрабатывают ступенчатое воздействие, но имеют постоянную ошибку при отработке линейно возрастающего сигнала (табл. 3). Эта ошибка
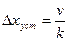 , (136)
, (136)
пропорциональна скорости v изменения входного сигнала, ввиду чего ее называют скоростной ошибкой, а коэффициент передачи разомкнутой системы k — добротностью системы по скорости. Отсутствие статической ошибки объясняется наличием в одноцепочечной структурной схеме системы интегрирующего звена.
Астатические системы 2-го порядка принципиально точно отрабатывают как ступенчатый, так и линейно возрастающий сигнал. При отработке квадратичного сигнала имеет место ошибка
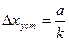 , (137)
, (137)
пропорциональная ускорению а входного сигнала и обратно пропорциональная коэффициенту усиления разомкнутой системы k, который называется добротностью системы по ускорению, а сама ошибка — ошибкой системы по ускорению.
Итак, с увеличением коэффициента передачи разомкнутой системы установившиеся ошибки уменьшаются. Но, как было показано в седьмой беседе, с увеличением k ухудшается устойчивость автоматических систем. Таким образом, требование к точности противоречит требованию к устойчивости. Следовательно, при выборе величины k должно быть принято компромиссное решение. Забегая наперед, отметим, что улучшение устойчивости при заданном относительно большом значении k достигается путем включения в систему корректирующих устройств, о чем подробно будет рассказано в девятой беседе.
Отмечая влияние порядка астатизма системы v на точность, констатируем, что чем больше v, тем точнее система отрабатывает более сложное воздействие. Поэтому следящие системы и системы управления выполняют как астатические. Однако с увеличением порядка астатизма системы более склонны к колебаниям в переходных процессах, и их устойчивость ухудшается. Поэтому системы с порядком астатизма более двух на практике почти не встречаются.
7. КОЭФФИЦИЕНТЫ ОШИБКИ
Если задающее воздействие является медленно меняющейся функцией времени, то динамическую ошибку можно вычислить при помощи так называемых коэффициентов ошибки. Покажем это.
Передаточную функцию ошибки можно представить рядом
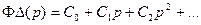 , (138)
, (138)
Тогда
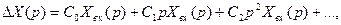 (139)
(139)
или в оригиналах
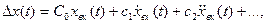 (140)
(140)
Таким образом, динамическая ошибка системы состоит из суммы слагаемых, пропорциональных входному сигналу, его скорости, ускорению и т. д., поэтому коэффициенты Со, С1, С2, ... называют коэффициентами ошибки соответственно По положению, по скорости, по ускорению и т. д.
Чем медленнее меняется входной сигнал, тем меньше надо брать членов ряда в формуле (140).
Известно несколько способов вычисления коэффициентов ошибки. Наиболее просто это сделать, разложив передаточную функцию ошибки в степенной ряд путем деления ее числителя на знаменатель.
Следует отметить, что порядок астатизма системы определяется количеством первых коэффициентов ошибки, равных нулю. Так, для статических систем (v = 0) ни один из коэффициентов не равен нулю, для астатических систем первого порядка С0 = 0, а для астатических систем второго порядка Со = 0 иС1 = 0.
8. ОШИБКИ ВЛИЯНИЯ ВОЗМУЩЕНИЯ
Для определения ошибок от возмущения структурную схему системы необходимо привести к виду, показанному на рис. 114, где Wp (p) и W0 (р) — передаточные функции частей системы, условно именуемых соответственно регулятором и объектом.
Передаточная функция по возмущению (рис. 114, б)
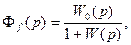
где W (р) = Wр (р) Wo (p) — передаточная функция разомкнутой системы.
Тогда изображение ошибки в соответствии с формулой (133)
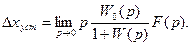 (141)
(141)
Пользуясь этой формулой, можно не только вычислить величину установившейся ошибки, но и определить порядок астатизма системы по отношению к возмущению. Так, в частности, если регулятор не содержит интегрирующего звена, то система будет статической, если содержит – то астатической (рис. 115).
Например, при статическом объекте и статическом регуляторе соответственно имеем 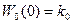 и
и 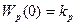 . При ступенчатом возмущении
. При ступенчатом возмущении 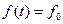 . С учётом того, что
. С учётом того, что 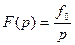 , установившаяся ошибка
, установившаяся ошибка
 (142)
(142)
|
Если же регулятор будет астатическим, т. е. Wp (р) = 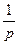 W*(p), причем W*p(0) = kp, то
W*(p), причем W*p(0) = kp, то
 (143)
(143)
т. е. система является астатической.
Читателю предлагается самому рассмотреть два аналогичных случая, если
объект регулирования будет астатическим.
Подведем итоги. Качество процессов регулирования — это обобщенная характеристика динамических свойств автоматических систем, которая определяется поведением системы как в переходных процессах, так и в установившихся режимах.
Переходный процесс обусловливается инерционностью системы. Его можно оценить прямо или косвенно. При прямой оценке тем или иным способом строят график переходного процесса, по которому находят основные его показатели. Косвенные оценки не требуют построения графика переходного процесса, и в этом их достоинство. Они позволяют определить некоторые черты переходного процесса и установить влияние параметров системы на качество переходных процессов.
Точность автоматических систем характеризует вынужденное движение, которое оценивается величиной установившейся ошибки. Эта ошибка зависит как от характера внешнего воздействия, так и от свойств самой системы. С увеличением коэффициента передачи разомкнутой системы ее ошибки уменьшаются, однако, при этом ухудшается устойчивость. Поэтому имеют место противоречивые требования к точности и устойчивости.
Показатели качества процесса регулирования должны удовлетворять предъявляемым к системам требованиям. Это достигается коррекцией динамических свойств системы
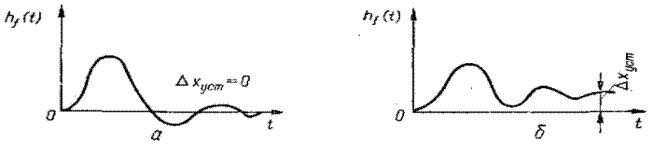 Рис. 115. Переходные функции и установившиеся ошибки по возмущению для астатических (а)
Рис. 115. Переходные функции и установившиеся ошибки по возмущению для астатических (а)
и статических (б) систем.
Дата добавления: 2015-07-14; просмотров: 1756;

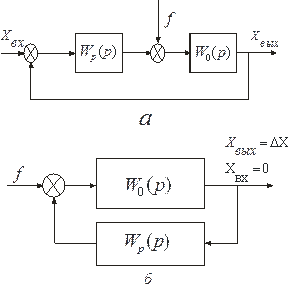 Рис. 114. Структурные схемы АС при наличии
задающего и возмущающего воздействий (а)
и только возмущающего воздействия (б).
Рис. 114. Структурные схемы АС при наличии
задающего и возмущающего воздействий (а)
и только возмущающего воздействия (б).