Общие методы

К числу общих методов повышения точности систем автоматического регулирования относятся:

1) увеличение коэффициента усиления разомкнутой цепи;

2) повышение степени астатизма;

3) применение регулирования по производным от ошибки. Увеличение общего коэффициента усиления разомкнутой цепи является

наиболее универсальным и эффективным методом. Увеличить общий коэффи­циент усиления можно обычно за счет введения в систему регулирования усилителей. Однако в некоторых случаях удается достичь этого увеличения за счет повышения коэффициентов передачи отдельных звеньев, например чувствительных элементов, редукторов и т. д.

Увеличение общего коэффициента усиления благоприятно сказывается в смысле уменьшения ошибок практически во всех типовых режимах. Это вытекает, в частности, из того, что общий коэффициент усиления разомкну­той цепи входит в качестве делителя во все коэффициенты ошибок (см. при­мер, рассмотренный в § 8.3).

Однако увеличение общего коэффициента усиления ограничивается устойчивостью системы регулирования. При повышении коэффициента уси­ления, как правило, система приближается к колебательной границе устой­чивости. При некотором предельном его значении в системе возникают неза­тухающие колебания. В этом сказывается противоречие между требованиями к точности и требованиями к устойчивости системы регулирования.

В связи с этим повышение общего коэффициента усиления до значения, нри котором обеспечивается выполнение требований к точности, обычно может производиться только при одновременном повышении запаса устойчи­вости системы, что осуществляется при помощи так называемых корректи­рующих средств, рассматриваемых в следующей главе.

Повышение порядка астатизма.Повышение порядка астатизма исполь­зуется для устранения установившихся ошибок в различных типовых режи­мах: в неподвижном положении, при движении с постоянной скоростью, при движении с постоянным ускорением и т. д. Формально это сводится к тому, чтобы сделать равными нулю первые коэффициенты ошибки системы, например, с₀ = 0 при астатизме первого порядка, или с₀ = с_± = 0 при астатизме второго порядка, или с₀ = с_х = с_% = 0 при астатизме третьего порядка и т. д. Физически повышение порядка астатизма осуществляется за счет введения в канал регулирования интегрирующих звеньев. В качестве таких звеньев могут, например, использоваться звенья, изображенные на рис. 4.21. Структурная схема системы регулирования с введенным интегрирующим звеном изображена на рис. 9.1. Передаточная функция инте­грирующего звена

,

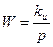Где k_и [ 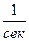] - коэффициент передачи интегрирующего звена. W (р) представляет собой передаточную функцию разомкнутой системы регулирования до введения интегрирующего звена.

Результирующая передаточная функция разомкнутой системы будет иметь дополнительный множитель р в знаменателе:

Wэ = ,

W(p) = ,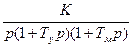

которая соответствует астатизму пер­вого порядка.

В соответствии с примером, рассмотренным в § 8.3, первые коэффициен­ты ошибки можно записать следующим образом (если положить Т_У = Т₁, Т_М = Т_2, К = К₀):

C₀ = 0,

C₁ = ,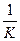

,

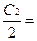
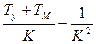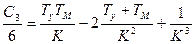
Введем в систему интегрирующее звено, например интегрирующий при­вод. Соответствующая этому случаю электромеханическая схема изображена на рис. 9.2. В этой схеме приняты следующие условные обозначения: СКВТ — синусно-косинусные вращающиеся трансформаторы, ЛВТ — линей­ный вращающийся трансформатор, Д — двигатели, Р — редукторы, ТГ — тахогенератор. Передаточная функция исходной системы без интегрирую­щего звена (9.1) была выведена в § 6.2. Передаточная функция разомкнутой системы, изображенной на рис. 9.2, будет отличаться от (9.1) наличием дополнительного множителя 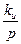, который дает интегрирующее звено. В результате получим передаточную функцию разомкнутой системы в виде:

W(p) = ,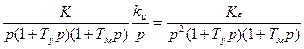

где К_ε = k_и К [ 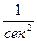] - добротность системы по ускорению.

Эта передаточная функция соответствует уже астатизму второго порядка. Передаточная функция системы по ошибке

Ф_о = 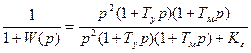(9.4)

Раскладывая эту функцию в ряд делением числителя на знаменатель, полу­чаем вместо (9.2) следующие равенства для коэффициентов ошибок:

C₀ = C₁ = 0, 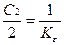, 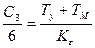(9.5)

Сравнивая (9.5) с (9.2), можно заметить, что в результате введения интегрирующего звена вследствие повышения порядка астатизма получено условие с_г = 0, и, следовательно, будет равна нулю

скоростная составляющая ошибки.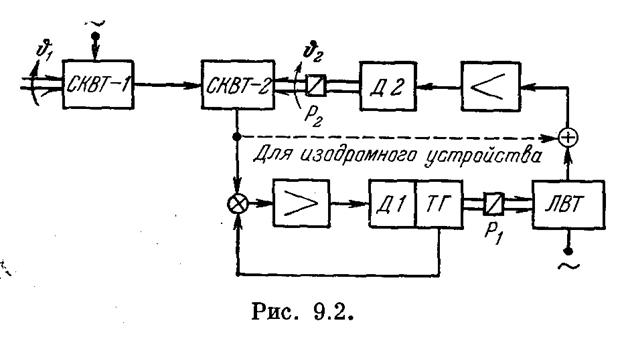

Однако, если йковерить теперь систему на устойчи­вость, можно убедиться, что система вообще не может ра­ботать, так как получить ус­тойчивую работу нельзя ни при каком зн^ении общего коэффициента усиления К_г.

Это называется структурной неустойчивостью. Действительно, передаточ­ной функции (9.3) соответствует характеристическое уравнение

в котором отсутствует член, содержащий оператор в первой степени. Пропуск одного из членов в характеристическом уравнении всегда соответствует неустойчивости в соответствии с § 6.1.

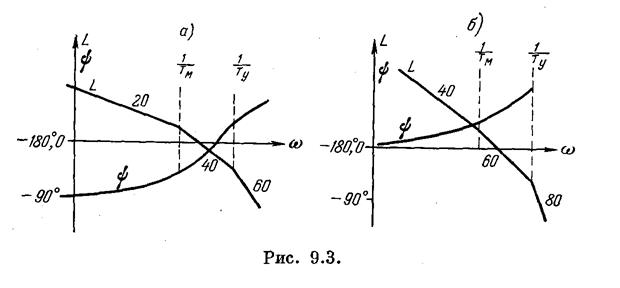
Появление неустойчивости в рассматриваемой системе при повышении порядка астатизма можно проиллюстрировать на логарифмических характе­ристиках. Логарифмические характеристики для передаточной функции (9.1) построены на рис. 9.3 по выражениям:

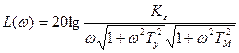
Логарифмические характеристики для передаточной функции (9.3) по­строены на рис. 9.3 по выражениям:

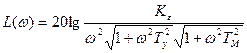
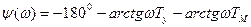
Сравнение рис. 9.3, а и 9.3, б, а также формул (9.7) и (9.9) показывает, что введение интегрирующего элемента дает дополнительный фазовый сдвиг {—90°), в результате чего в рассматриваемой схеме нельзя добиться устой­чивой работы ни при каком значении общего коэффициента усиления. Однако это не означает, что схема явля­ется вообще неработоспособной. Введение в нее корректирующих средств (см. главу 10) позволяет не только достичь устойчивости, но и обеспечить определенный за­пас устойчивости, т. е. выполнить требования к качеству процесса регулирования.

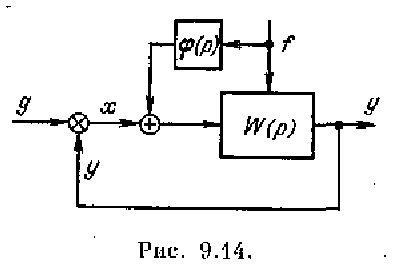
Применение изодромных уст­ройств. Существует путь повыше­ния порядка астатизма системы регулирования без заметного или недо­пустимого ухудшения ее запаса устойчивости. Этот путь заключается в при­менении изодромных устройств, например таких, как изображенные на рис. 4.22. Структурная схема системы регулирования при введении изо­дромного устройства изображена на рис. 9.4. Передаточная функция изо­дромного устройства может быть представлена в виде

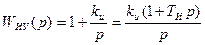
Где, 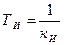постоянная времени изодромного устройства.

Пример введения изодромного устройства показан на рис. 9.5. На рис. 9.5, а изображен чувствительный элемент регулятора давления.

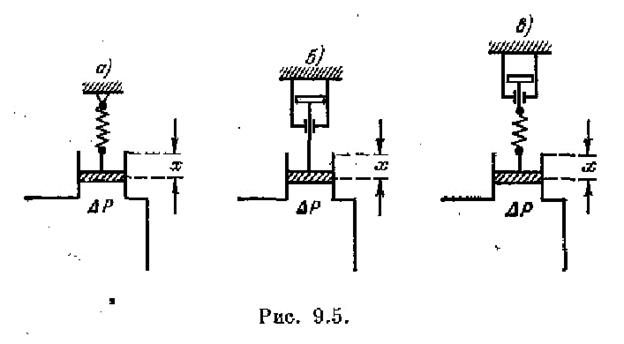
с противодействующей пружиной. Если не учитывать массу движущихся частей, то перемещение чувствительного элемента будет пропорциональным отклонениюдавления от заданного значения:

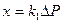
Где, к₁ - коэффициент пропорциональности, определяемый жесткостью пружины.

На рис. 9.5, б изображен тот же элемент, но с противодействующим демпфером. Так как сила, развиваемая демпфером, пропорциональна скоро­сти перемещения его поршня, то в этом случае будет иметь место соотношение рх =к₂.∆P Вместо (5.11) получим

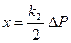
где к₂ — коэффициент, определяемый скоростным сопротивлением демпфера. Равенство (9.12) соответствует введению интеграла в закон регулиро­вания.

Наконец, в случае, изображенном на рис. 9.5, в, перемещение чувстви­тельного элемента будет складываться из деформации пружины и перемеще­ния поршня демпфера:

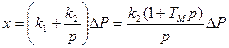
Т_И — постоянная времени изодромного устройства. В качестве второго примера рассмотрим приведениую выше схему следя­щей системы (рис. 9.2). Переход от ведения дополнительного интеграла к ведению изодромного устройства может быть сделан добавлением связи, показанной пунктиром. Передаточная Функция разомкнутой системы может быть получена умножением (9.1)

На передаточную функцию изодромного устройства.

В результате для рассматриваемой схемы получим:

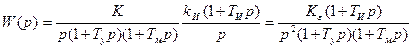
Где, Кε = к_{и *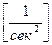} - добротность системы по ускорению.

Коэффициенты ошибки определяются равенствами:

С₀ = С₁ = 0, ,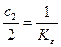

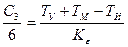
Рассматривая характеристическое уравнение системы:

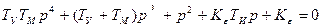
можно убедиться, что в системе возможно получение устойчивости при выполнении условия:

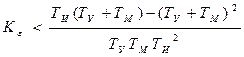
Или в ином виде:

Нетрудно видеть, что при Т_И, стремящемся к бесконечности (это будет при отсутствии интегри­рующего привода в изодромном механизме) условие устойчивости переходит в неравенство

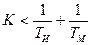
которое справедливо для исходной схемы_т изображенной на рис. 6.4. При достаточно больших значениях постоянной времени изодромного механизма Т_И , что соответствует малому передаточному коэффициенту интегрирующего привода 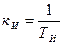, условия устойчивости (9.16) и (9,7) будут мало отличаться от условия устойчивости (9,18) исходной схемы. Таким об­разом, введение изодромного ме­ханизма с относительно большой постоянной времени Т_И дает повы­шение порядка астатизма на еди­ницу при возможности практиче­ски сохранить условия устойчиво­сти в системе, куда этот механизм вводится. Это обстоятельство можно про­иллюстрировать также на лога­рифмических частотных характеристиках (рис. 9,6). В соответствии с вы­ражением для передаточной функции разомкнутой системы (9.14) можно записать:

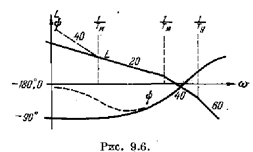
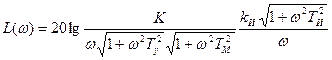
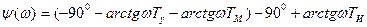
Сравнивая эти выражения с формулами (9.6) и (9,7) справедливыми дл» исходной схемы, можно заметить, что при относительно большом значе­нии постоянной времени Т_ж логарифмические характеристики системы с изодромным устройством будут иметь отличие только в низкочастотной области при . Для частот 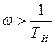— дополнительный множитель

в (9.19) обращается в единицу, а дополнительный фазовый сдвиг в (9.20) равен нулю. Таким образом, при 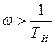-логарифмические частотные характеристики; системы с изодромным устройством практически не отличаются от логарифмических характеристик исходной схемы. В частности, в районе нуля децибел для л. а. х. можно получить одинаковый вид амплитудной и фазовой характеристик для обеих схем, что будет соответствовать одина­ковому запасу устойчивости.

На рис. 9.6 сплошными линиями показаны л. a. x_t и л, ф. х. для исход­ной схемы_т а пунктирными — изменения, даваемые введением изодромного-устройетва с относительно большой постоянной времени.

Следует заметить, что введение изодромного устройства с большой постоянной времени образует систему, динамические качества которой могут оказаться сравнительно низкими. Это объясняется тем, что введение такого устройства улучшает вид амплитудной характеристики только в низкочастот­ной области (рис, 9.6). В результате коэффициенты ошибки, следующие за тем коэффициентом, который обращается в нуль, могут не только не умень­шиться, ио даже возрасти,

В рассмотренном выше примере при введении изодромного устройства обратился в нуль коэффициент c_t (9.15), Однако в следующие коэффициенты

в качестве делителя входит добротность по ускорению 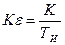. При большом значении постоянной времени Т_И добротность системы по ускорению К_Е получается малой и коэффициенты ошибок с₃, с_а, ... сильно возрастают.

Для дальнейшего повышения порядка астатизма системы регулирова­ния могут применяться не один а два, три и т. д. изодромных устройства. В этом случае можно получить повышение порядка астатизма на один, два, три и т, д. в зависимости от необходимости. На рис. 9.7 в качестве примера приведена структурная схема системы с тремя изодромными устройствами, т. е. схема с тройным изодромированием. Если исходная система имеет,

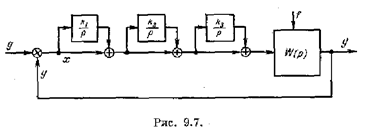
например, астатизм первого порядка, го система рис. 9.7 с изодромными устройствами будет обладать астатизмом четвертого порядка. В этом слу­чае для коэффициентов ошибок будет иметь место равенство с_а = c_f — с₂ = — c_s = 0. Как и ранее, при соответствующем выборе постоянных времени 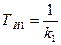, , 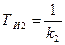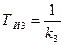можно сохранить практически те же условия устойчивости, что и в исходной системе. Регулирование по производным от ошибки. В большинстве случаев регулирование по производным от ошибки имеет целью повысить запас

устойчивости системы, что позво­ляет увеличить общий коэффициент усиления системы и тем самым улучшить точность регулирования. Это будет рассмотрено более по­дробно в главе 10.

Однако регулирование по про­изводным от ошибки может само­стоятельно повышать точность сис­темы регулирования даже в том случае_т когда сохраняется неиз­менным общий коэффициент усиления в системе. Физика этого явле­ния заключается том, что при введении регулирования по производ­ным система начинает чувствовать не только наличие ошибки, но и тенденцию к изменению ее величины. В результате система регулирования более бистро реагирует на появление задающих и возмущающих воздействий, что сни­жает ошибку регулирования.

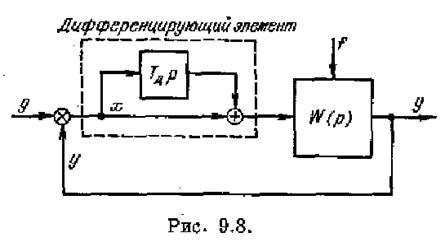
Структурная схема введения производной по ошибке изображена на рис. 9.8. Передаточная функция части прямого канала вместе с включенным дифференцирующим элементом может быть представлена приближенно (в предположении, что дифференцирующий элемент является идеальным) в виде

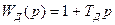
где Г_д — постоянная времени дифференцирующей цепи. В качестве дифференцирующих элементов могут, например, применяться устройства, изображенные на рис, 4.23 и 4.24.

Рассмотрим в качестве примера ту же систему (рис. 6.4). При введении производной от ошибки при помощи тахогенераторов, уста­новленных на командной и исполнительной осях ,электромеханическая схема.

будет иметь вид, изображенный на рис. 9.9. Здесь приняты следующие обозначения: СКВТ — синусно-косинусные вращающиеся трансформаторы, ТГ — тахогенераторы, Д — двигатель, Р — редуктор. Передаточная функция разомкнутой системы может быть получена умножением (9.1) на передаточную функцию (9,21). В результате получим

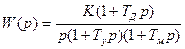
где постоянная времени Т_ц представляет собой отношение передаточного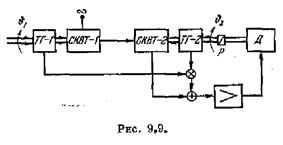

коэффициента тахогенератора к передаточному коэффициенту чувствительного элемента (СКВТ), т. е.

.

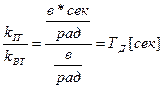Для передаточной функции разомкнутой системы (9.22) находим пере­даточную функцию по ошибке:

Ф_о =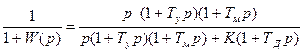

Раскладывая ее в ряд, получаем соотношения для коэффициентов ошибок:

C₀ = 0,

C₁ = ,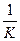

,

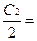
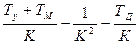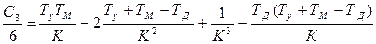
Сравнивая последние выражения с (9.2), можно заметить, что коэффи­циенты с₄ и с_в (а так же следующие коэффициенты) уменьшаются при введе­нии регулирования по первой производной от ошибки. При соответствующем выборе величины постоянной времени Т_я можно добиться условий с_а = О или с₃ — 0. При с₂ — 0 система не будет иметь установившейся ошибки» пропорциональной ускорению.

Аналогичным: образом, применяя два включенных последовательно дифференцирующих элемента, можно получить равенство нулю одновре­менно двух коэффициентов, например с_а = 0 и с₃ — 0. В этом случае можно показать, что в системе, наряду с регулированием по первой производной от ошибки, будет использоваться регулирование по второй производной. Это вытекает из того_, что передаточная функция двух дифференцирующих элементов, включенных ,'друг за другом в соответствии с рис, 9,8, будет равна произведению двух передаточных функций типа (9,21):

9.25

Где τ_± = Т_Д1 + Т_Д2 представляет собой отношение коэффициентов передачи по первой производной и по ошибке, а - отношение коэффициентов передачи по второй производной и по ошибке.

Как видно из рассмотренного, в отличие от случая введения изодромного устройства (см. рис, 9,4), когда обращается в нуль первый, ранее отличный от нуля коэффициент ошибки, введение дифференцирующего элемента (рис. 9.8) не влияет на этот коэффициент ошибки, но зато уменьшает после­дующие коэффициенты. В связи с этим наиболее эффективное снижение ошибки системы регулирования может быть достигнуто при одновременном использовании изодромных устройств и дифференцирующих элементов.

Так как дифференцирование эквивалентно дополнительному усилению верхних частот, то использование более чем двух дифференцирующих эле­ментов оказывается затруднительным вследствие возрастания влияния высо­кочастотных помех. Число же изодромных устройств ограничивается только получающимся усложнением системы регулирования. Однако и оно обычно не превышает грех.

§ 9,2. Теория инвариантности и комбинированное управление

Одним из способов, позволяющих получить высокую точность в системах автоматического регулирования, является использование методов так назы­ваемой теории инвариантности [74, 129]. Система автоматического регули­рования является инвариантной по отношению к возмущающему воздействию, если после завершения переходного процесса, определяемого начальными условиями, регулируемая величина и ошибка системы не зависят от этого воздействия. Система автоматического регулирования является инвариант­ной по отношению к задающему воздействию, если после завершения пере­ходного процесса, определяемого начальными условиями, ошибка системы не зависит от этого воздействия.

Оба этих понятия имеют общую математическую трактовку. Рассмотрим эту трактовку для случая, когда на систему действует одно входное воздей­ствие — задающее g (t) или возмущающее / (2). Пусть для ошибки системы регулирования имеет место дифференциальное уравнение

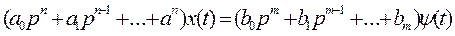9.26

Где ψ(е) — задающее или возмущающее воздействие, а 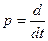. Решение этого уравнения имеет две составляющие — переходную x_П (t) и вынужденную x_В {t). Переходная составляющая определяется общим реше­нием уравнения (9.26) без правой части, а вынужденная — частным решени­ем уравнения (9.26) с правой частью.

Изображение ошибки х (t) при нулевых начальных условиях можно представить в следующем виде:

, ,

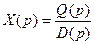Где

,

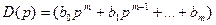
Здесь введено также изображение функции времени ψ{t), представляю­щее собой дробно-рациональную функцию комплексной величины р = с + jω.

,

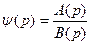В соответствии с теоремой разложения (см. § 7,4) оригинал (9.27) в случае отсутствия кратных корней может быть представлен в виде:

,

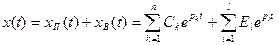где р_к — полюсы передаточной функции, т. е. корни уравнения D (р) = О, a pi — полюсы входного воздействия, г. в. корни уравнения В (р) = 0.

Вынужденная составляющая x_в (t) будет тождественно равна нулю в следующих случаях.

1. Если A (р) = 0, то х_& (t) ≡ 0. Этот случай является тривиальным, так как соответствует отсутствию входного воздействия, и он не представляет интереса.
2. Если Q {р) — 0, то также х_Б (t) ≡ 0. Этот случай соответствует абсо­лютной инвариантности системы по отношению к входному воздействию ψ(t), которое может быть любой функцией времени, т. е. меняться по произволь­ному закону.

В следящих системах при рассмотрении задающего воздействия условие Q (p) = 0 означает, что равна нулю передаточная функция по ошибке: Ф_x (р )= 0. В иной записи это означает равенство единице передаточной функции замкнутой системы: Ф (р) = 1 -- Ф_х (р) = 1, Это условие приводит к тому, что следящая система должна иметь бесконечную полосу пропуска­ния, так как частотная передаточная функция замкнутой системы Ф (jω) = i при всех частотах 0 < ω < ∞. В реальных системах реализовать бесконеч­ную полосу пропускания невозможно, поэтому реализация абсолютной инвариантности по задающему воздействию сталкивается с принципиаль­ными трудностями.

Заметим, что в случае, когда следящая система должна воспроизводить задающее воздействие в некотором масштабе к, условие абсолютной инва­риантности запишется в виде Ф (р) = к. Однако это не меняет существа дела.

При рассмотрении возмущающего воздействия условие Q (р) = 0 озна­чает равенство нулю передаточной функции по возмущающему воздействию: Ф_F (р) =; 0. Здесь в принципе возможно получение абсолютной инвариант­ности по данному возмущению, однако в большинстве случаев приходятся иметь дело со значительными техническими трудностями.

1. Равенство нулю вынужденной составляющей будет наблюдаться для таких входных функций, изображения которых имеют все полюсы, т. е. все корни уравнения В (р) = 0, совпадающие с нулями передаточной функ­ции, т.е. с корнями уравнения Q (р) = 0. В этом случае после разложения на множители полиномов В{р) и Q (р) можно сократить одинаковые сомно­жители вида (р — р_i) в числителе и знаменателе изображения (9.27). В ре­зультате второе слагаемое в выражении (9.29) обращается в нуль и х_В (t) ≡ 0.

Этот случай соответствует частичной инвариантности. Система будет инвариантна к входным воздействиям определенного вида, например к воз­действиям, которые могут быть представлены в виде степенной функции времени с положительными и ограниченными степенями, в виде суммы экспо­нент с заданными постоянными времени и т. п..

Вводится также понятие инвариантности системы по отношению к ка­кому-либо входному воздействию с точностью до е. Здесь имеется в виду не тождественное равенство нулю вынужденной составляющей ошибки x_В{t), а приближенное равенство, мерой выполнения которого является некоторая величина е. Для оценки выполнения инвариантности до е суще­ствуют различные критерии, сливающиеся практически с критериями точ­ности систем регулирования, рассмотренными в главе 8.

Основным методам, используемым при построении инвариантных систем, является применение так называемого комбинированного управления.

Комбинированное управление. Под комбинированным управлением или регулированием понимается такой метод построения замкнутых автомати­ческих систем, когда, наряду с регулированием по отклонению или ошибке, используется регулирование по задающе­му или возмущающему воздействию. Та­ким образом, в системе комбинирован­ного управления осуществляется регу­лирование по замкнутому и разомкну­тому циклам.

Рассмотрим вначале случай, когда дополнительно к регулированию по от­клонению х {t) используется регулирова­ние по задающему воздействию g (t). Струк­турная схема такой системы изображена на рис. 9.10, а.

В случае отсутствия регулирования по задающему воздействию, т. е. при Ф (р) = 0, регулируемая величина у связана с задающим воздействием g через передаточную функцию замкнутой системы,

,

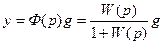Где W(p) – передаточная функция разомкнутой системы.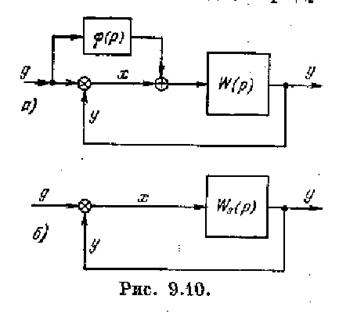

При введении регулирования по задающему воздействию регулируемая" величина определяется выражением

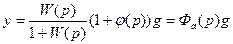
Эквивалентная передаточная функция замкнутой системы с учетом регулирования по задающему воздействию:

,

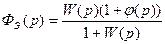Из последнего выражения видно, в частности, что введение регулирова­ния по задающему воздействию не меняет характеристического уравнения системы, работающей по отклонению, так как знаменатель передаточной функции замкнутой системы одинаков в (9.30) и (9.32). Это обстоятельство является замечательным свойством систем комбинированного регулирования.

Введение дополнительного регулирования по задающему воздействию не меняет левой части дифференциального уравнения. Это означает что не будут нарушаться не только условия устойчивости, но сохранятся оценив качества переходного процесса, базирующиеся на использовании корней характеристического уравнения.

Из выражения (9.32) по известным, соотношениям (5.19) и (5.26) могут быть найдены эквивалентная (т. е. с учётом регулирования по задающему воздействию), передаточная функция по ошибке.

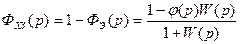
и передаточная функция разомкнутой системы

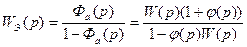
Переход к эквивалентной передаточной функции разомкнутой системы W$ (р) позволяет заменить структурную схему системы комбинированного управления эквивалентной ей обычной схемой системы регулирования,. работающей но отклонению (рис. 9.10* 6).

Из формулы (9,33) для передаточной функции по ошибке можно» найти условие полной инвариантности системы регулирования. Положив Фхэ (р) = O получаем:

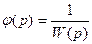9.35

Разложив последнее выражение в ряд по возрастающим степеням опера­тора, получим необходимый вид функции, определяющей вводимый сигнал от управляющего воздействия:

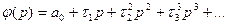9.36

Где a₀ - безразмерное число.

Этот ряд может быть конечным и бесконечным. Первое слагаемое (9.36) в астатических системах и в большинстве статических систем (см. следующий параграф) оказывается равным нулю. Это не распространяется на случай ис­пользования комбинированного управ­ления по возмущающему воздействию, где практически всегда получается a ≠ 0.

Таким образом» при введении регу­лирования по задающему воздействию для получения полной инвариантности необходимо вводить первую и высшие про- ■-, извод ныв от задающего воздействия.

Обычно точно можно ввести только в некоторых случаях первую произ­водную, а все последующие производные могут быть получены приближенно при помощи использования известных дифференцирующих звеньев (см.» например, рис. 4.23 и 4.24). Поэтому практически может быть получена не полная, а частичная инвариантность. Это соответствует введению огра­ниченного числа первых членов разложения: (9.36).

Так, например, введением первой производной от задающего воздей­ствия в системе с астатизмом первого порядка можно получить равной нулю скоростную ошибку, г. е. повысить степень астатизма относительно задаю­щего воздействия па единицу. Вводя первую и вторую производные (даже приближенно), можно повысить степень астатизма на два и т. д. Это дает обращение в нуль соответствующих коэффициентов ошибки (8.20),

В некоторых случаях сигнал по задающему воздействию может вводиться, но непосредственно на вход системы, как это показано на рис. 9.10, а в неко­торую точку внутри канала регулирования (рис. 9.11),

В этом, более общем, случае эквивалентная передаточная функция замк­нутой системы будет иметь вид.

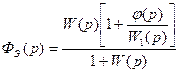9.37

Эквивалентная передаточная функция по ошибке:

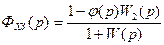9.38

Эквивалентная передаточная функция разомкнутой системы:

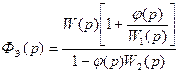
Условие полной инвариантности

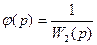
В качестве примера рассмотрим следящую систему (см. рис. 6.4) при введении регулирования по первой производной от угла поворота командной.

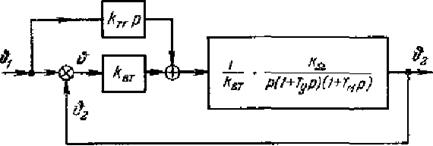
оси, которое осуществляется при помощи тахогенератора. Электромеханиче­ская и структурная схемы для этого случая изображены на рис. 9.12.

В соответствии с общим случаем, изображенным на рис. 9.11, имеем:

, , .

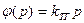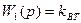Эквивалентная передаточная функция замкнутой, системы (9.37)

,

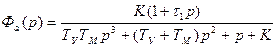Где 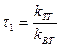- постоянная времени цепи первой производной от угла поворота командной оси.

Эквивалентная передаточная функция по ошибке (9.38)

.

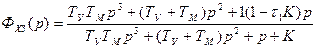Скоростная ошибка будет равна нулю в том случае, когда в числителе последнего выражения будет равен нулю коэффициент при операторе в пер­вой степени. Отсюда получаем условие частичной инвариантности (ликвида­ция скоростной ошибки):

,

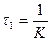Из (9.39) можно найти эквивалентную передаточную функцию разом­кнутой системы:

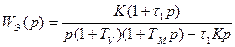
При выполнении условия (9.41) эквивалентная передаточная функция разомкнутой системы будет соответствовать астатизму второго порядка:

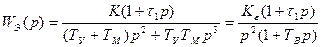
Где 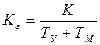- добротность системы по ускорению, 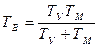-эквивалентная постоянная времени.

В качестве второго примера рассмотрим инерциальную вертикаль (рис. 9.13, а). Принцип работы ее заключается в том, что акселерометр Л воспринимает ускорение перемещения подвижного объекта, на котором установлена стабилизированная платформа (СЛ), и составляющую ускорения силы тяжести, возникающую при наклоне этой платфор­мы на некоторый угол а (ошибка вертикали). Таким образом, акселерометр оп­ределяет ускорение

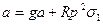9.42

Где g – ускорение силы тяжести, R – радиус Земли.σ₁ - путь пройденный объектом по Земле в дуговых единицах. Это ускорение дважды интегрируется и поступает па стабилизированную плат­форму, которая поворачивается на угол

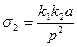9.43

где k₁ и к₂. — коэффициенты передачи первого и второго интеграторов. К зтим двум уравнениям необходимо добавить связь между ошибкой вертикали а, пройденным путем в дуговых единицах σ₁ и углом поворота стабилизированной платформы σ₂.

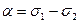9.44

Для рассмотренных уравнений (9.42) — (9.44) инерциальной вертикали изобразим структурную схему (рис, 9.13,6). Сравнивая ее с рис. 9.11, можем записать:

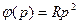, 9.45

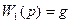, 9.46

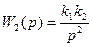, 9.47

Условие полной инвариантности (9.40):

,

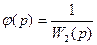откуда следует, что должно быть выполнено равенство 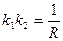передаточная функция разомкнутой системы. Тогда передаточная функция разомкнутой системы:

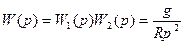. 9.48

а передаточная функция по ошибке будет тождественно равна нулю: Ф_ХЗ (p) = 0. Следовательно, при любых движениях объекта, на котором установлена инерциальная вертикаль, ошибка вертикали будет равна нулю. Это будет справедливым в том случае, если выполнены нулевые начальные условия, т. е. отсутствует свободное движение вертикали под действием начальных условий, ив случае, когда можно считать, что достаточно точно

выполняется требуемое условие 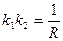. Заметим, что в рассмотренном случае особенно важно иметь нулевые начальные условия вследствие того, что передаточной функции (9.48) соот­ветствует характеристическое уравнение.

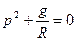. 9.49

Оно имеет чисто мнимые корни:

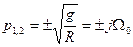9.50

где Ω₀ — частота незатухающих колебаний инерциальной вертикали, которой соответ­ствуй период Т ≈ 84,6 мин, называемый периодом Шулера. При наличии ненулевых начальных условии в системе будут устанавливаться незатухающие колебания с частотой Ω₀, что бу­дет нарушать работу вертикали. Комбинированное управление может быть использовано также для сни­жения ошибки от возмущающего воздействия (рис. 9.14). В этом случае наряду с регулированием по отклонению х (t) используется регулирование по возмущающему воздействию f(t). Передаточная функция по возмущению здесь будет иметь вид:

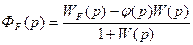, 9.51

Где W_F — передаточная функция по данному возмущению в разомкнутой системе, W (р) — передаточная функция разомкнутой системы. Условие полной инвариантности может быть получено, если положить Ф_F (р) = 0- Тогда:

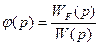, 9.52

Эта функция также может быть представлена в виде ряда, аналогично формуле (9.36):

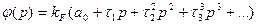, 9.53

Где a₀ - безразмерное число (1 или 0), a k_F — некоторый коэффициент, размерность которого совпадает с размерностью передаточной функции. Как и в случае использования регулирования но задающему воздействию получение полной инвариантности затрудняется необходимостью вводить первую и более высокие производные от возмущения / (I). Поэтому используется, как правило, частичная инвариантность, получающаяся при реализации в системе регулирования первых членов разложения (9.53). Это в свою очередь дает обращение в нуль соответствующих первых коэффи­циентов ошибки но возмущению (с₀, с_и с₂ и т. д.).

Б заключение заметим, что возможно использование комбинированных систем с введением регулирования ио нескольким возмущающим воздействи­ям и получением полной или частичной инвариантности по каждому из них. Однако это приводит, конечно, к усложнению схемы.