Задача про ланцюги

Теорія графів почалася з розв’язування задачі про кенігсберзькі мости (Ейлер, XVIII ст.). Розташування мостів в м. Кенігсберг наведено на рис.8.

Рис. 8.

В місті є 7 мостів {a, b, c, d, e, f, g}, які його розбивають на чотири частини {A, B, C, D}. Необхідно обійти всі мости міста, проходячи по кожному рівно один раз, і повернутись у початкову точку.

Граф для цієї задачі наведений на рис.9.

Рис.9.

Загальна постановка задачі є наступною (Ейлер): в яких випадках у скінченному неорієнтованому графі можна знайти такий цикл, у якому кожне ребро графу зустрічалось би рівно один раз. Якщо такий цикл існує, то він називається ейлеревим циклом, а сам граф називається ейлеревим.

Твердження. Скінченний граф G(V) є ейлеровим тоді і тільки тоді, коли:

1) G(V) - зв’язний граф;

2) локальні степені всіх його вершин парні.

Алгоритм побудови ейлеревого циклу:

1) вибираємо довільну вершину a Î V;

2) будуємо довільний ланцюг P з початком у вершині „a”. Оскільки локальні степені всіх вершин графу є парні, то ланцюг може завершитись тільки в „a” (тобто він є циклом);

3) якщо P(a, a) містить не всі ребра графу G(V), то будуємо граф G₁ = G ‑ P(a, a), в якому всі вершини мають теж парний локальний степінь. Оскільки граф G(V) є зв’язним, то серед вершин P(a, a) має знайтись вершина „b”, яка зв’язана ребром хоча б з однією вершиною графу G(V) (інакше граф G був би незв’язним);

4) будуємо з ребер графу G₁ ланцюг P’, що починається у вершині „b” і може закінчуватись тільки у „b”; з ланцюгів P і P’ будуємо новий цикл:

P₁(a, a) = P(a, b) È P’(b, b) È P(b, a);

5) якщо P₁(a, a) не містить всіх ребер графу G(V), то, за аналогією з кроком 3) будуємо граф G₂ = G – P₁(a, a) і т.д.

З огляду на скінченність графу, цей процес зупинитися, коли всі ребра графу G(V) будуть вичерпані.

Узагальнюючи задачу Ейлера можна шукати найменшу кількість ланцюгів (не циклів!) P₁, які не перетинаються по ребрах і покривають увесь зв’язний граф G(V).

Твердження. Нехай G(V) - скінченний зв’язний граф з k вершинами непарного локального степеня. Тоді мінімальна кількість ланцюгів, які не перетинаються по ребрах і покривають граф G, дорівнює k / 2.

Алгоритм побудови ланцюгів P_i.

1) з’єднуємо довільно чином пари вершин з непарним локальним степенем (для цього необхідно k / 2 ребер). При цьому утворюється граф G₁, всі вершини якого мають парний степінь;

2) граф G₁ є ейлеровим і в ньому існує ейлерів цикл S;

3) після відкидання з циклу S доданих на кроці 1) k / 2 ребер, отримуємо k / 2 ланцюгів, які покривають весь граф G.

Приклад

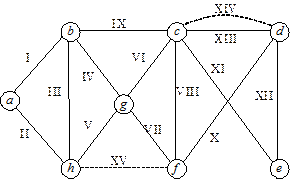
Рис. 10.

Степені вершин графу:

Таким чином, k = 4. З’єднаємо ребрами вершини (c, d) та (f, h) (на рис.10 ці ребра позначені штриховими лініями).

Поетапно побудуємо для утвореного графу цикл Ейлера:

а) P₁ = (І, ІІІ, ІІ);

б) P₂ = (І, ІХ, VI, IV, III, II);

в) P₃ = (І, IX, XIII, XII, XI, VI, IV, III, II);

г) P₄ = (I, IX, XIV, X, VIII, XIII, XII, XI, VI, IV, III, II);

д) P₅ = (I, IX, XIV, X, VIII, XIII, XII, XI, VI, VII, XV, V, IV, III, II).

Віднімаючи додані раніше ребра XIV і XV, отримаємо три ланцюги:

1) (І, Х);

2) (Х, VIII, XIII, XII, XI, VI, VII);

3) (V, IV, III, II).

Зауважимо, що перший і третій ланцюги мають спільний кінець – вершину „а”. „Склеюючи” ці ланцюги, отримаємо остаточно:

1) (V, IV, III, II, I, IX);

2) (X, VIII, XIII, XII, XI, VI, VII).

Для орієнтованих графів має місце

Твердження. Нехай G(V) - орієнтований зв’язний граф. Граф G містить ейлерів цикл тоді і тільки тоді, коли у кожну вершину v входять стільки ж ребер, скільки і виходить:

r(v) = r*(v).

Якщо в неорієнтованому графі кожне неорієнтоване ребро замінити двома орієнтованими і протилежно направленими, то мають місце умови попереднього твердження і тому правильне таке

Твердження. У скінченному зв’язному неорієнтованому графі завжди можна побудувати орієнтований цикл, який проходить через кожне ребро по одному разу в кожному з двох напрямків.