Двочасткові графи

Граф G =(V,E ) називається двочастковим, якщо існує розбиття {V₁,V₂} множини вершин V на дві підмножини (частки) таке, що для довільного ребра (v,w)ÎE виконується або v ÎV₁ i w ÎV₂, або v ÎV₂ i w ÎV₁.

Двочастковий граф G =(V,E ) називається повним двочастковим графом, якщо для будь-якої пари вершин його часток v ÎV₁ i w ÎV₂ маємо (v,w)ÎE. Якщо |V₁|=m i |V₂|=n, то повний двочастковий граф G позначається K_m,n.

Теорема (теорема Кеніга). Граф є двочастковим тоді і тільки тоді, коли всі його цикли мають парну довжину.

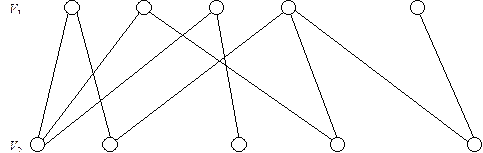
Визначення. Нехай G(V₁, V₂) - дводольний граф. Пароз’єднання – це підмножина ребер графу G:{(x_i, y_j), …}, де x_i Î V₁ а y_j Î V₂, причому жодні два ребра не мають спільних вершин.

Визначення. Максимальне пароз’єднання (П) – це пароз’єднання дводольного графу G, яке має найбільшу кількість ребер.

Розглянемо таку задачу: знайти максимальне пароз’єднання, яке містить всі вершини множини V₁.

Твердження (теорема Холла). Максимальне пароз’єднання П дводольного графу покриває всі вершини множин V₁ тоді і тільки тоді, якщо для довільної множини U₁ Í V₁ кількість елементів у множині U₂ Í V₂, яка містить всі вершини, з’єднані ребром хоча б однією вершиною з U₁, не менша від кількості вершин множини U₁.

Алгоритм побудови максимального пароз’єднання П.

Будемо вважати, що умови теореми Холла виконані. Задамося довільним пароз’єднанням П₀. Якщо воно не охоплює всіх вершин множини V₁, то існує x₀ : x₀Î V₁ і x₀Ï П₀.

Побудуємо

W₀ = {x₀};

W₁ = {y | (x₀, y) Î G};

W₂ = {x | (x, y) Î П₀, y Î W₁, x Ï W₀};

W₃ = {y | (x, y) Î G, x Î W₂, y Ï W₁};

W₄ = {x | (x, y) Î П₀, y Î W₃, x Ï W₀ È W₂};

W₅ = {y | (x, y) Î G, x Î W₄, y Ï W₁ È W₃};

. . .

Зауважимо, що, згідно з побудовою, в множинах W₁ і W₂, W₃ і W₄, W₅ і W₆ і т.д. попарно однакова кількість елементів. Крім того, послідовність вершин W_i не може закінчитись на множині з парним індексом W_2k, оскільки для множини

U₁ = W₀ È W₂È … È W_2k Í V₁

кількість вершин у відповідній множині

U₂ = W₁ È W₃È … È W_{2k - 1} Í V₂

(U₂ містить всі вершини графу, які з’єднані ребром хоча б з однією з вершин множини U₁) на одиницю більше, що суперечить умові теореми Холла. Тому існує вершина y*:

y* Î W_{2k - 1} і y* Ï П₀.

Тоді існує шлях S, який починається з x₀, проходить через вершини множин W₁ і закінчується в y* і містить непарну (2k ‑ 1) кількість ребер:

S = {e₁, e₂, …, e_{2k - 1}},

причому всі парні ребра e_2k Î П₀.

Нове пароз’єднання П₁ будуємо наступним чином:

П₁ = П₀ \ {e₂ È e₄ È…È e_{2k - 2}} È {e₁ È e₂ È…È e_{2k - 1}}.

Пароз’єднання П₁ містить на одне ребро і на одну вершину з множини V₁ більше ніж П₀. Якщо П₁ охоплює всі вершини множини V₁, то беремо деяку вершину x₀ : x₀Î V₁ і x₀Î П₁ і т.д.

Приклад

П₀ = {(x₁, y₁), (x₃, y₂)}.

1) W₀ = (x₂); W₁ = (y₂); W₂ = (x₃); W₃ = (y₁); W₄ = (x₁); W₅ = (y₄).

e₁ = (x₂, y₂); e₂ = (x₃, y₂); e₃ = (x₃, y₁); e₄ = (x₁, y₁); e₅ = (x₁, y₄).

П₁ = {(x₂, y₂), (x₃, y₁), (x₁, y₄)}.

2) W₀ = (x₄); W₁ = (y₃, y₄).

e₁ = (x₄, y₃).

П = П₂ = {(x₁, y₄), (x₂, y₂), (x₃, y₁), (x₄, y₃)}.

5. Плоскі та планарні графи

У багатьох випадках не має особливого значення, як зобразити граф у вигляді рисунка на площині (діаграми), оскільки ізоморфні графи подібні за своєю структурою і містять ту саму інформацію. Однак існують ситуації, коли необхідно, щоб зображення графа на площині задовольняло певні умови. Наприклад, якщо граф є моделлю деякої електронної схеми або транспортної мережі, де вершинами є окремі елементи схеми або станції, а ребрами, відповідно, - електричні провідники і шляхи, то бажано так розташувати ці ребра на площині, щоб уникнути перетинів.

Таким чином виникає поняття плоского графа.

Граф називається плоским, якщо його діаграму можна зобразити на площині так, що лінії, які відповідають ребрам графа, не перетинаються (тобто мають спільні точки тільки у вершинах графа). Таке зображення називається плоскою картою графа.

Граф називають планарним, якщо він ізоморфний деякому плоскому графу.

Наприклад, граф, зображений на рис., планарний, оскільки він ізоморфний графу, зображеному поруч. Простий цикл, дерево і ліс - це також планарні графи.

Про планарні графи кажуть, що вони укладаються на площині або мають плоске укладання.

а) б)

Рис.

При дослідженні плоских графів особливе місце займають графи K₅ i K_3,3, зображені на рис.

K₅ K_3,3

Рис.

Граф K_3,3 виникає із задачі про три хати і три криниці.

Теорема. Графи K₅ i K_3,3 не є планарними.

Значення графів K₅ i K_3,3 полягає в тому, що вони є "єдиними" суттєво непланарними графами. Всі інші непланарні графи містять у собі підграфи "подібні" до K₅ або K_3,3. Характер цієї подібності розкривається за допомогою таких понять.

Елементарним стягуванням графа G =(V,E ) називається вилучення в графі G деякого ребра (v_i,v_j)ÎE і злиття вершин v_i i v_j в одну вершину v, причому v інцидентна всім тим відмінним від (v_i,v_j) ребрам графа G, які були інцидентні або v_i , або v_j.

Кажуть, що граф G стягується до графа G ¢, якщо G ¢ можна отримати з G за допомогою послідовності елементарних стягувань.

Приклад . На рис. зображено графи G i G ¢, при цьому G стягується до G ¢.

G G ¢

Рис.

Наведемо без доведення важливу теорему теорії графів.

Теорема (теорема Куратовського). Граф G є планарним тоді і тільки тоді, коли він не містить підграфів, що стягуються до K₅ або K_3,3.