Деякі класи графів

Дерева

Дерева - це особливий і дуже важливий клас графів. Особлива роль дерев визначається як широким їхнім застосуванням у різних галузях науки і практики, так і тим особливим положенням, яке дерева займають у самій теорії графів. Останнє випливає з граничної простоти будови дерев. Часто при розв’язуванні різних задач теорії графів їхнє дослідження починають з дерев. Зокрема, порівняно нескладною є проблема перевірки ізоморфності дерев.

Твердження 1. В дереві дві довільні вершини зв’язані єдиним ланцюгом (інакше був би цикл).

Твердження 2.Довільний ланцюг у дереві є простим.

Визначення. У довільному графі G вершина v називається кінцевою, якщо r(v) = 1, тобто існує одне ребро, інцидентне вершині v, і це ребро називається кінцевим.

Твердження 3. У дереві є хоча б дві кінцеві вершини.

Розглянемо дерево G і виберемо довільну вершину v₀. Кожному ребру e = (a, b) зіставимо той кінець, який більш віддалений від v₀ (оскільки в дереві всі ланцюги є простими, то від довільної вершини до v₀ веде лише один ланцюг).

Твердження 4.Для дерева виконується рівність v_V – v_E = 1 (v_V - кількість вершин, v_E - кількість ребер).

Твердження 5. У дереві кожне ребро суттєве (його вилучення веде до порушення зв’язаності графа).

Визначення. В довільному скінченному зв’язаному графі G циклічний ранг:

g(G) = v_E ‑ v_V + 1.

Твердження. Для довільного скінченного зв’язаного графа G циклічний ранг

g(G) ³ 0

і дорівнює кількості ребер, які необхідно вилучити з G для того, щоб отримати дерево (скелет графа).

Для дерев g(G) = 0.

Дерева використовують для розв’язання такої задачі: необхідно з’єднати „n” міст залізничною колією таким чином, щоб не будувати зайвих ліній. При цьому вважається відомим вартість будівництва колії між двома довільними містами. Таким чином, необхідно побудувати зв’язний граф G, який містить всі задані вершини і для якого повна вартість 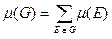була б найменшою. Очевидно, що граф G - дерево.

Алгоритм розв’язання.

Вибираємо ребро e_i з найменшою вартістю. Отримаємо граф A₁ = {e₁}. На кожному наступному кроці до A_{i ‑ 1} додаємо ребро, яке має найменшу вартість серед тих, що залишились, і таке, що граф A_i = A_{i ‑ 1} È {e_i} не має циклів. Останній граф A_{n ‑ 1} = G і є шуканим.