Алгоритм Дейкстри.
Масиви, що використовуються:
VID: VID(i) – найкоротша на даний момент відстань від s до i -ї вершини графу;
FIX: FIX(i) = 1, якщо i-та вершина графу є фіксованою;
PRED: PRED(i) містить передостанню вершину в найкоротшому з усіх відомих на даний момент шляхів від s до і-ї вершини графу.
1) Початкові установки.
Для початкової вершини: VID(s) = 0, FIX(s) = 0, PRED(s) = s.
Для всіх інших вершин графу: VID(v) = ¥, FIX(v) = 0, PRED(v) = v.
Біжуча вершина: u = s, i = 1.
2) Цикл по тих вершинах графу G, для яких FIX(v) = 0
якщо існує e = (u, v) і VID(u) + d(u, v) £ VID(v)
то VID(v) = VID(u) + d(u, v), PRED(v) = u.
3) Серед вершин графу G, для яких FIX(v) = 0, знаходимо ту вершину v0, для якої
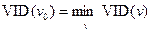 .
.
4) FIX(v0) = 1, u = v0.
5) i = i + 1.
якщо i £ n,
то йти на 2).
6) Кінець.
В результаті масив VID містить найкоротші відстані від s до всіх вершин графу; по масиву PRED можна отримати найкоротший шлях від s до довільної вершини графу.
Приклад.
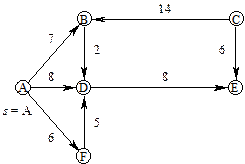
Рис.7
Робота алгоритму проілюстрована в табл. 5, в якій кожний рядок відповідає одному циклу роботи алгоритму. Фіксовані вершини підкреслені, а біля вершини „u” на кожному кроці стоїть зірочка.
Таблиця 5
| i | VID | PRED | ||||||||||
| A | B | C | D | E | F | A | B | C | D | E | F | |
| 0* | ∞ | ∞ | ∞ | ∞ | ∞ | A | B | C | D | E | F | |
| ∞ | ∞ | 6* | A | A | C | A | E | A | ||||
| 7* | ∞ | ∞ | A | A | C | A | E | A | ||||
| ∞ | 8* | ∞ | A | A | C | A | E | A | ||||
| ∞ | 16* | A | A | C | A | D | A | |||||
| ∞ | A | A | C | A | D | A |
Найкоротший шлях від A, наприклад, до E будується, використовуючи масив PRED, таким чином: E D A.
Дата добавления: 2015-08-26; просмотров: 627;
