Відстань, діаметр, радіус і центр графу

Нехай G - зв’язний, неорієнтований граф. Оскільки дві довільні вершини „a” і „b” – зв’язані, то в загальному випадку існує декілька простих ланцюгів S_i(a, b), які з’єднують „a” і „b”. В цій множині ланцюгів має існувати ланцюг, який має найменшу довжину. Ця найменша довжина і називається відстанню між „a” і „b”: d(a, b). Будемо вважати за визначенням, що d(a, a) = 0.

Введена відстань задовольняє всі аксіоми метрики:

1) d(a, b) ³ 0;

2) d(a, b) = 0 тоді і тільки тоді, коли a = b;

3) d(a, b) = d(b, a);

4) d(a, b) + d(b, c) ³ d(a, c).

Для скінченного графу можна ввести поняття діаметру.

Визначення. Діаметр графу G(V):

.

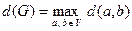Виберемо деяку вершину c Î V і позначимо через

,

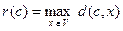віддаль від с до найбільш віддаленої вершини графу.

Назвемо c₀ центром графу G, якщо

.

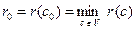Зауважимо, що центр графу не єдиний.

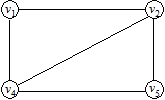
Рис.6

Наприклад, для графу, зображеного на рис. 6, радіус r₀ = 1; центр графу c₀ = v₂ або c₀ = v₄.