Зв’язаність

Нехай G - неорієнтований граф.

Визначення. Дві вершини „a” і „b” графу G називаються зв’язними, якщо існує маршрут S(a, b).

Якщо в S(a, b) деяка вершина v_i повторюється більше одного разу, то відкидаючи циклічну ділянку S(v_i, v_i), отримаємо новий маршрут S’(a, b), в якому вершина v_i зустрічається тільки один раз. Повторюючи цю процедуру для всіх таких вершин v_i, приходимо до висновку: якщо дві вершини в графі можуть бути зв’язані маршрутом, то існує і простий ланцюг, який зв’язує ті ж вершини.

Визначення. Граф G називається зв’язним, якщо зв’язна будь-яка його пара вершин.

Всі підграфи G(V_i) зв’язного графу G(V) є теж зв’язними і називаються зв’язними компонентами графу.

Зауважимо, що зв’язність – відношення еквівалентності між вершинами графу:

а) довільна вершина v графу зв’язана сама з собою;

б) якщо „a” і „b” – зв’язні (тобто існує маршрут S(a, b)), то в силу неорієнтованості графу „b” і „а” теж зв’язані (маршрутом S(b, a));

в) якщо зв’язані „а” і „b” (маршрутом S₁(a, b)) і „b” і „с” (маршрутом S₂(b, c)), то існує маршрут з „а” в „с” (S₁(a, b) + S₂(b, c)), тобто вершини „a” і „c” теж зв’язані.

В силу відомого твердження з алгебри, граф G розбивається на класи еквівалентності – підграфи, в яких всі вершини є зв’язаними між собою і які не мають спільних вершин:

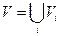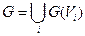, (пряма сума)

таким чином, істинне

Твердження. Довільний неорієнтований граф розбивається на пряму суму своїх зв’язаних компонент.

Це дозволяє більшість задач зводити до випадку зв’язаних графів.