Частини, суграфи і підграфи графу.

Операції з частинами графу

Визначення. Граф Н називається частиною графу G (позначається H Í G), якщо:

а) V(H) Í V(G);

б) E(H) Í E(G).

Визначення. Граф Н називається суграфом графу G, якщо він є частиною графу G і

V(H) = V(G).

На Рис. 4 зображені граф G і його три частини. Граф H3 є суграфом.

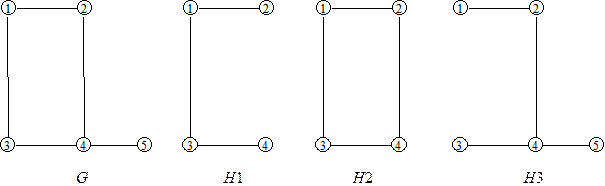
Рис.4.

Визначення. Суграф H називається покриваючим для графу G, якщо будь-яка вершина H інцидентна хоча б одному ребру з G. Зауважимо, що якщо в графі G є ізольовані вершини, то для нього не існує покриваючого графу H.

Визначення. Підграфом G(U) графу G(V) називається така його частина, яка містить всі ребра графу G(V), що з’єднують дві будь-які вершини з множини U.

На рис. 4 H1 не є підграфом G (не містить ребро e(2, 4)), а H2 – підграф графу G.

Визначення. Зірковим графом, який визначається деякою вершиною a Î V, називається граф, що містить всі ребра даного графу G(V), інцидентні вершині „a”.

За аналогією з операціями поміж множинами можна виконувати і операції між графами.

Визначення. Якщо H – частина графу, то 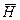(доповнення графу H) – це граф, в який входять всі ребра графу G, які не належать H:

.

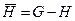Визначення. Нехай H₁ і H₂ - дві частини графу G. Тоді H = H₁ È H₂ (об’єднання або сума) це також частина графу G, яка складається зі всіх ребер, що належать або H₁ або H₂.

Визначення. Нехай H₁ і H₂ - дві частини графу G. Тоді H = H₁ Ç H₂ (перетин) це частина графу G, яка складається зі всіх ребер, що належать H₁ та H₂ одночасно.

Визначення. Якщо дві частини H₁ і H₂ графу G не мають спільних вершин, то їх сума H = H₁ È H₂ називається прямою. Якщо H₁ і H₂ не перетинаються по ребрах, то їх сума називається прямою по ребрах.

Наприклад: 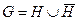- пряма сума за ребрами.