Способи задання графів
Графічний опис графів є незручним для їх аналізу на ЕОМ. Тому розглянемо табличні способи задання графів.
Надалі будемо розглядати тільки скінченні графи, у яких множини вершин V = {v1, …, vn} і ребер E = {e1, …, em} є скінченними.
Визначення. Матриця суміжності вершин графу G(V) (позначається M(G) = {Mij}) - це квадратна матриця розміру n´n, в якій Mij - кількість ребер, які з’єднують Vi з Vj в графі G. Якщо граф G неорієнтований, то
Mij = Mji,
тобто матриця М є симетричною.
На рис.2 зображений деякий неорієнтований граф; відповідна матриця суміжності вершин приведена в табл.1.
 Рис.2
Рис.2
| Таблиця 1 | ||||||
Граф також може бути описаний за допомогою матриці інцидентності (позначається N(G) = {Nij}), яка має n рядків (вершини) і m стовпців (ребра). Для неорієнтованого графу Nij = 1, якщо вершина vi інцидентна ребру ej; в протилежному випадку - Nij = 0.
Для орієнтованого графу Nij = 1, якщо vi - початкова вершина ребра ej; Nij = ‑1, якщо vi - кінцева вершина ребра ej; Nij = 0, якщо вершина vi не інцидентна ребру ej.
У табл. 2 наведена матриця інцидентності для неорієнтованого графу, зображеного на рис. 2.
На рис. 3 зображений орієнтований граф, матриця інцидентності для якого наведена в табл. 3.
Неорієнтований граф без петель G може бути також описаний квадратною матрицею суміжності ребер (позначається I(G) = {Iij}) розміром m´m, причому Iij = 1, якщо i ¹ j і у ребер ei і ej є спільна вершина. В протилежному випаду - Iij = 0.
Для графу, зображеного на рис. 2, відповідна матриця суміжності ребер приведена в табл. 4.
Таблиця 2
| І | ІІ | ІІІ | IV | V | VI | VII | VIII | IX | |
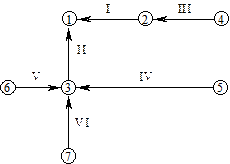 Рис. 3
Рис. 3
| Таблиця 3 | |||||
| І | ІІ | ІІІ | IV | V | VI | |
| -1 | -1 | |||||
| -1 | ||||||
| -1 | -1 | -1 | ||||
Таблиця 4
| І | ІІ | ІІІ | IV | V | VI | VII | VIII | IX | |
| І | |||||||||
| ІІ | |||||||||
| ІІІ | |||||||||
| IV | |||||||||
| V | |||||||||
| VI | |||||||||
| VII | |||||||||
| VIII | |||||||||
| IX |
Дата добавления: 2015-08-26; просмотров: 941;
