Гомоморфізми та ізоморфізми алгебр

Розглянемо алгебри A(X; j₁, …, j_k) і B(Y; y₁, …, y_k), в яких операції j_l та y_l є однаково n_i ‑ арними, i = 1, 2, …, k. Відображення f: X ® Y з умовою 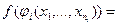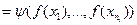для всіх та всіх називається гомоморфізмом алгебри A(X; j₁, …, j_k) в алгебру B(Y; y₁, …, y_k). Гомоморфізм, який є одночасно бієктивним відображенням, називається ізоморфізмом алгебр.

Множина Y Í X називається замкнутою відносно n-арної операції j на Х, коли j(Yⁿ) Í X. Якщо підмножина Y Í X замкнута відносно всіх операцій алгебри A(X; j₁, …, j_k) і їй відповідає алгебра B(Y; y₁, …, y_k), то остання називається підалгеброю алгебри A(X; j₁, …, j_k).

Для випадків груп та кілець поняття гомоморфізму, ізоморфізму та підалгебри були розглянуті раніше.