Кільця та поля

Нехай К – непорожня множина, на якій задані дві бінарні алгебраїчні операції + (додавання) і ∙ (множення), які задовольняють наступним умовам:

(K1) (K, +) – абелева група;

(К2) (K, ∙) – півгрупа;

(К3) операція множення дистрибутивна відносно операції додавання:

(x + y) z = x z + y z, z (x + y) = z x + z y

для всіх x, y, z Î K.

Тоді (K, +, ∙) називається кільцем.

Структура (K, +) називається адитивною групою кільця, а (K, ∙) - його мультиплікативною півгрупою.

Якщо (K, ·) – моноїд, то кажуть, що (K, +) – кільце з одиницею. Кільце називається комутативним, якщо (K, ∙) – абелева півгрупа (на відміну від груп, комутативне кільце не прийнято називати абелевим). Нейтральний елемент 0 – відносно додавання і 1 – відносно множення (якщо він існує) називають відповідно нулем і одиницею кільця.

Далі наведено приклади кілець:

1) множина (Z, +, ∙) цілих чисел відносно звичайних операцій додавання й множення;

2) множина (Q, +, ∙) раціональних чисел відносно звичайних операцій додавання й множення;

3) множина (R, +, ∙) дійсних чисел відносно звичайних операцій додавання й множення;

4) множина (C, +, ∙) комплексних чисел відносно звичайних операцій додавання й множення;

5) множина дійснозначних матриць М_n(R) розміру nxn відносно додавання та множення матриць є кільцем з одиницею. Роль нейтрального елемента відносно множення тут відіграє одинична матриця Е. Таке кільце називається повним матричним кільцем над R або кільцем квадратних матриць порядку n над R. Це один з найважливіших прикладів кілець. Оскільки при n > 1, матриці при множенні, як правило не можна переставляти, то М_n(R) – некомутативне кільце.

Підмножина L кільця К називається підкільцем, якщо для будь-яких елементів x, y Î L

x + y Î L i x ∙ y Î L.

Підкільце L кільця К з одиницею називається ідеалом, коли для будь-яких елементів x Î L та a Î K виконується a∙x Î L, x∙a Î L.

Нехай К - кільце з одиницею, а L – ідеал у цьому кільці. Фактор-групу К / L адитивної групи (K, +) кільця за ідеалом L (який є нормальним дільником в адитивній групі) можна перетворити в кільце, наступним чином задаючи операцію множення суміжних класів: (x + L) · (y + L) = x∙y + L. Це кільце називається фактор-кільцем кільця К за ідеалом L і позначається К / L.

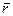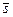Нижче наведено приклад фактор-кільця, який широко використовується. Множина nZ цілих чисел, кратних деякому фіксованому натуральному числу n, є ідеалом в кільці цілих чисел Z. Розглянуту раніше фактор-групу Z / nZ = Z_n можна перетворити в кільце задаючи операцію множення Ä класів за модулем числа n. Щоб перемножити два класи і потрібно спочатку перемножити цілі числа r і s, а потім знайти остачу від ділення знайденого добутку на число n. Клас знайденої остачі й буде результатом множення класів 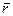і 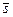. Множина Z_n разом із заданими на ній операціями додавання Å та множення Ä є комутативним кільцем з одиницею, яке має n елементів.

Далі наведено таблицю Келі для операції множення Ä кільця Z₅:

Ä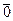

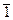
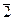
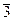
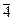
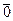
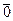
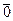
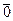
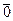
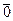
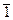
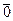
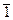
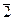
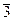
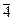
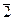
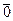
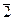
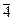
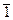
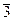
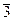
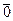
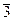
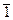
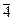
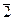
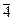
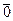
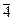
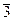
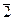
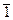
Відображення f: К₁ ® К₂ кільця (К₁, +, ∙) в кільце (К₂, Å, Ä) називається гомоморфізмом, якщо воно зберігає всі операції, тобто коли для будь-яких елементів x, y Î К₁

f(x + y) = f(x) Å f(y),

f(x ∙ y) = f(x) Ä f(y).

Якщо гомоморфізм кілець є бієктивним відображенням, то він називається ізоморфізмом кілець. Два кільця К₁ i К₂ називаються ізоморфними, якщо існує ізоморфізм кільця К₁ в кільце К₂; факт ізоморфізму кілець коротко записують у вигляді К₁ @ К₂.

Поле Р – це комутативне кільце з одиницею, в якому кожен відмінний від нуля елемент має обернений відносно операції множення. Іншими словами комутативне кільце з одиницею Р є полем, коли сукупність його відмінних від нуля елементів утворює абелеву групу відносно операції множення.

Два поля Р₁ i Р₂ називаються ізоморфними, якщо вони ізоморфні як кільця.

Поле, яке має скінченне число елементів, називається скінченним полем або полем Галуа.

Теорема. Будь-яке скінченне поле має рⁿ елементів, де р – просте, а n – натуральне число. Для фіксованих простого числа р і натурального числа n існує і, з точністю до ізоморфізму, лише одне поле з числом елементів рⁿ.

Скінченні поля з точністю до ізоморфізму будуються наступним чином.

Скінченне поле з р елементів ізоморфне кільцю Z_p цілих чисел за модулем р.

Скінченне поле з рⁿ елементів отримується таким чином. Розглядаємо кільце многочленів Z_p[x] від змінної х над полем Z_p. Беремо в цьому кільці многочлен f(x) степеня n, який є нерозкладним над Z_p. Позначаємо через (f(x)) ідеал, який складається з елементів, що діляться на f(x). Тоді фактор-кільце Z_p[x]/(f(x)) є бажаним полем з рⁿ елементів. Виконання операцій над елементами цього поля здійснюється за двома модулями: за модулем числа р і за модулем многочлена f(x). Часто це позначається наступним чином: (mod f(x), p).