Інтерференція світла в тонких плівках. Кільця Ньютона
Не слід вважати, що інтерференцію світла можна спостерігати лише в лабораторних умовах із застосуванням спеціального обладнання. Кожному з нас не раз доводилось спостерігати за свіченням мильних плівок, олійних плям на поверхні води, кольори гартованих предметів, кольори найтонших металевих покрить фарфорових виробів, різноколірність крил різних метеликів, бджіл тощо. В усіх цих випадках інтерференція світла спостерігається в досить тонких прозорих плівках, товщина яких близька до довжини хвилі і перебуває в межах довжини когерентності.
Розглянемо плоско паралельну прозору плівку товщиною 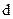 , на яку падає під кутом
, на яку падає під кутом 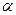 плоска монохроматична хвиля.
плоска монохроматична хвиля.
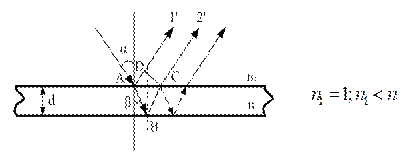
Рис. 5
Плівка має товщину 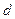 (рис. 5) і показник заломлення
(рис. 5) і показник заломлення 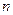 . Падаюча хвиля в точці А ділиться на дві частини, одна з яких 1', змінивши фазу на протилежну, відбивається під кутом
. Падаюча хвиля в точці А ділиться на дві частини, одна з яких 1', змінивши фазу на протилежну, відбивається під кутом 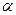 до перпендикуляра в точці падіння. Друга частина 2' після заломлення у точці A і C відбивається в точці B. Далі промені 1' і 2' поширюються паралельно.
до перпендикуляра в точці падіння. Друга частина 2' після заломлення у точці A і C відбивається в точці B. Далі промені 1' і 2' поширюються паралельно.
Накладання променів 1' і 2' здійснюється на сітківці ока спостерігача. Результати інтерференції залежать від оптичної різниці ходу цих променів.
Знайдемо оптичну різницю ходу променів 1' і 2', яка відповідно до рис. 5 буде дорівнювати
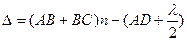 , (22)
, (22)
де 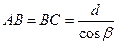 ;
; 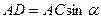 ;
; 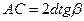 .
.
Підставивши значення цих величин в (22), одержимо
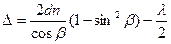 ,
,
або
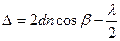 . (23)
. (23)
Формула (23) дає залежність оптичної різниці ходу хвиль від кута заломлення 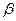 і параметрів плівки.
і параметрів плівки.
Знайдемо залежність оптичної різниці ходу хвиль 1' і 2' від кута падіння 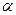 , вважаючи що
, вважаючи що
 і що
і що  .
.
Тому
 ,
,
або
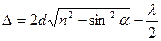 . (24)
. (24)
В залежності від того, яке число півхвиль вкладається в оптичній різниці ходу хвиль 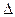 , плівка буде світлою (умова max) або темною (умова min).
, плівка буде світлою (умова max) або темною (умова min).
Важливо знати:
1. При освітленні плівки білим світлом для деяких хвиль виконується умова max, а для деяких – умова min. Тому плівка буде забарвлена певним кольором.
2. Колір плівки залежить від кута падіння променя, а тому полоси інтерференції в цьому випадку називаються полосами однакового нахилу.
3. Можливість ослаблення білого світла внаслідок інтерференції широко використовується у сучасних оптичних приладах (фотоапаратах, біноклях тощо). Для цього на поверхню лінзи наносять тонкий шар прозорої плівки з показником заломлення, меншим, ніж у лінзи, і більшим, ніж у повітря. Товщину прозорої плівки беруть такою, щоб мінімуми інтерференції спостерігалися в середній частині видимого спектра ( 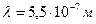 ). Таку оптику називають просвітленою (рис.6).
). Таку оптику називають просвітленою (рис.6).
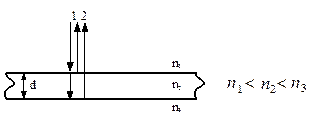
Рис. 6
Промінь 1 при відбиванні від поверхні плівки змінив фазу на протилежну. Промінь 2 двічі пройшов товщину плівки 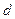 і при відбиванні на нижній частині плівки теж змінив фазу на протилежну. Оптична різниця ходу в плівці буде дорівнювати
і при відбиванні на нижній частині плівки теж змінив фазу на протилежну. Оптична різниця ходу в плівці буде дорівнювати
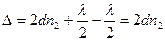 .
.
Якщо в 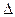 вкладається непарне число півхвиль, то промені від плівки не відбиваються, тобто спостерігається умова min.
вкладається непарне число півхвиль, то промені від плівки не відбиваються, тобто спостерігається умова min.
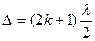 – умова min.
– умова min.
Окремим видом інтерференції світла є інтерференція в повітряному зазорі у вигляді клина між опуклою стороною плоско опуклої лінзи і поверхнею плоскої пластинки (рис. 7).
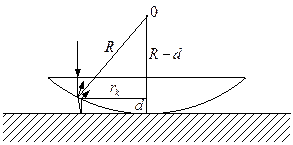
Рис. 7
Промені 1 і 2 одержані з одного променя, а тому є когерентні. Оптична різниця ходу променів у повітряному зазорі дорівнює
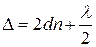 , (25)
, (25)
де n – показник заломлення середовища між лінзою і плоско паралельною пластинкою;
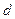 – товщина зазору в указаному місці.
– товщина зазору в указаному місці.
Промені 1 і 2 є відбитими, тому розглядається результат інтерференції у відбитому світлі. Аналогічно можна розглянути інтерференцію світла у прохідному світлі. В цьому випадку фаза поміняється на протилежну, а різниця ходу на 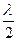 .
.
Знайдемо радіуси світлих і темних кілець Ньютона у відбитому світлі.
Для світлих кілець 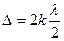 , а для темних кілець
, а для темних кілець 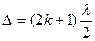 , де
, де 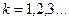
Радіус k-го кільця визначаємо з рисунка, де розглядаємо прямокутний трикутник.
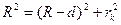 , (26)
, (26)
або
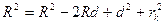 .
.
Нехтуючи нескінченно малою величиною 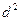 , одержимо
, одержимо
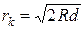 . (27)
. (27)
Для знаходження радіусів світлих кілець необхідно оптичну різницю ходу для променів у зазорі прирівняти до умови max, тобто
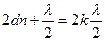 ,
,
звідки
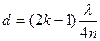 ,
, 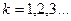 ,
,
тому
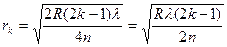 . (28)
. (28)
Вираз (28) дає радіуси світлих кілець Ньютона.
Для темних кілець
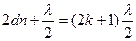 ,
,
звідки
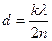 ,
,
тому
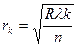 ,
, 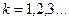 (29)
(29)
Вираз (29) визначає радіуси темних кілець Ньютона.
Важливо знати:
1. Правильна форма кілець Ньютона легко спотворюється при різних, навіть незначних, дефектах при шліфуванні різних поверхонь. Тому спостереження форми кілець Ньютона є найтоншим контролем якості шліфування поверхонь.
2. Явище інтерференції світла використовується у ряді дуже точних вимірювальних приладів, які називаються інтерферометрами. В цьому випадку точність вимірювань лінійних розмірів сягає 10-8 мм.
3. Кільця Ньютона утворюються в зазорі між опуклою лінзою і плоско паралельною пластинкою при однаковій (різна для різних кілець) товщині зазору. Тому полоси інтерференції, якими є кільця Ньютона, носять назву полоси однакової товщини.
Дата добавления: 2015-08-26; просмотров: 2133;
