Степінь вершини графа
Нехай G(V) - неорієнтований граф.
Визначення. Степенем r(a) деякої вершини a Î V називається кількість ребер графу, інцидентних цій вершині.
Якщо граф заданий матрицею суміжності вершин, то
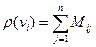(1)
Для матриці інцидентності аналогічна формула має вигляд
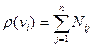(2)
Число ребер у графі G позначимо через vE = vE(G). При підрахунку суми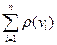 
кожне ребро e(vi, vj), графу G підраховується двічі: один раз – як таке, що з’єднує вершину vi з vj, а другий раз – як таке, що з’єднує vj з vi. Тому
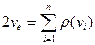(3)
(формула (3) залишається правильною і для графу з петлями, якщо їх розглядати як подвійні ребра).
Оскільки в лівій частині формули (3) стоїть парне число, то це означає, що у скінченному графі без петель кількість вершин з непарним степенем – парна.
Визначення. Граф називається однорідним степеня k, якщо r(vi = k), для всіх vi Î V.
В однорідному графі кількість ребер згідно з формулою (3) vE = nk/2.
Визначення. Повний граф U = U(V) - це неорієнтований граф, у якому дві довільні вершини з’єднані рівно одним ребром.
Зрозуміло, що повний граф U(V) з n вершинами – це однорідний граф степеня (n ‑ 1). Тому vE = n(n – 1) / 2.
Визначення. Повний граф з петлями U0 = U0(V) - це повний граф, у якому до кожної вершини додана петля.
Кількість ребер у повному графі з петлями vE(U0) = vE(U) + n = n(n + 1) / 2.
Нехай тепер G(V) - орієнтований граф. Тоді через r(vi) і r*(vi) позначають кількість ребер, які виходять з вершини vi і входять в вершину vi відповідно.
Аналогічно попередньому кількість ребер в орієнтованому графі
.
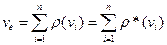Дата добавления: 2015-08-26; просмотров: 1164;