Понятие графа

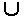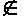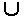Направленным графом называется тройка G = (V, E, Ф), где V - множество вершин, Е – множество дуг, а Ф – функция из Е в (V {w})², w V. Дуга е называется входом графа, если Ф(е) = (w, u), для u V {w}; внутренней, если Ф(е) = (u₁, u₂) для u₁,u₂ V; выходом, если Ф(е) = (u,w), для u V 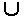{w}. Дуга е, являющаяся одновременно и входом и выходом графа, называется висячей; для нее Ф(е) = (w,w). Дуги, не являющиеся внутренними, называются также свободными.

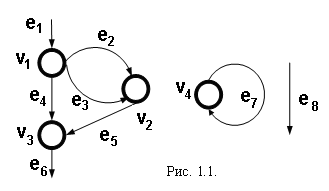Говорят, что дуга е инцидентна вершине u, если е выходит из u или ведет в u. Две дуги смежны, если существует хотя бы одна инцидентная им обеим вершина. Вершина u называется наследником вершины u', если в графе имеется хотя бы одна такая дуга, что Ф(е) = (u', u).

Изображенный на рисунке 1.1. граф G₁ содержит 4 вершины, 8 дуг. Дуга е₁ – входная, дуга е₆ – выходная, дуга е₈ – висячая, остальные дуги внутренние; вершины u₁ и u₃ наследники вершины u₁.

Путем в графе G называется последовательность …u_ie_iu_i+1… дуг и вершин, такая, что для всех i Ф(е_i) = (u_i,u_i+1). Образом пути называется слово, составленное из пометок проходимых дуг и вершин.

Две вершины u₁,u₂ графа G называются связанными, если u₁ = u₂ или существует маршрут е₁, …, е_n графа G такой, что дуга е₁ инцидентна вершине u₁, а дуга е_n – вершине u₂.