Функции. Отношение f называется функцией из А в В (из А на В), если df = A, rf В(rf = В) и для всех x, y1, y2 из <x

Отношение f называется функцией из А в В (из А на В), если d_f = A, r_f 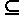В(r_f = В) и для всех x, y₁, y₂ из <x, y₁> f и <x, y₂> f следует y₁ = y₂. Обозначение f: A B. Пишем y = f(x) вместо <x, y> f и называем y значением функции f при значении аргумента х.

Функция f: A B осуществляет взаимно однозначное соответствие межу А и В, если d_f= A, r_f= В и из того, что y = f(x₁), y = f(x₂) следует х₁ = х₂.

Пусть А и В – частично упорядоченные множества и f – функция из А в В. f называется монотонным отображением, если из х₁ х₂ следует f(x₁) f(x₂) для всех x₁, x₂ А.

Функцию f: X Y называют n-местной функцией над множеством А, если Y = A и X = Aⁿ.

Предикатом называют функцию, областью значений которой является множество символов-цифр {0, 1}. При этом говорят, что предикат P: X {0, 1} истинен для x X, если P(x) = 1, и ложен, если P(x) = 0. Отношение на множестве Х – это двухместный предикат P: X² {0, 1}.

Алфавитом называют непустое конечное множество символов. Например, V₁ = {a, b}, V₂ = {0, 1}, V₃ = {a, +, 1, =} – алфавиты. Словом в алфавите V называется конечный объект, получаемый выписыванием одного за другим символов V, например, а + 1 = 1 + а – слово в алфавите V₃, 101011 – слово в алфавите V₂, abaab – слово в алфавите V₁. Длина слова – число символов в нем, пустое слово не содержит ни одного символа.

Множество всех слов в алфавите V обозначается V^*.

n-местной словарной функцией над алфавитом V называют n-местную функцию над V^*, т. е. функцию из 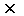V^* V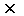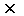^* … V^* (n раз) в V^*.