ОПТИМИЗАЦИЯ НА ГРАФАХ

Многие прикладные задачи оптимизации могут быть сформулированы в форме той или иной задачи оптимизации на графах. Наряду с этим в теории графов многие интересные задачи связаны с решением задач оптимизации.

Из достаточно большого числа типовых задач оптимизации на графах можно выделить основные и в некотором смысле ставшие классическими для данного класса:

q задача нахождения оптимальных покрывающих деревьев;

q задача нахождения кратчайшего пути в графе;

q задача нахождения критического пути в сетевом графе;

q задача нахождения максимального потока в графе.

Для каждой из перечисленных задач поставлена в соответствие математическая постановка задачи в форме модели булева или целочисленного программирования. В то же время существуют специальные алгоритмы их решения, которые учитывают специфические особенности постановки этих задач.

Рассмотрим более подробно содержательную постановку задачи о максимальном потоке в сети. Данная задача имеет множество возможных вариантов постановки, один из которых может быть сформулирован следующим образом. Имеется система магистральных трубопроводов, связывающих источник добычи нефти или газа с предприятием по его промышленной переработке (рис. 15.1). Отдельные участки трубопроводов оснащены компрессорными установками для поддержания требуемого давления, необходимого для транспортировки продукта. Известны предельные значения пропускной способности каждого участка рассматриваемой системы. В предположении, что источник обладает достаточным запасами продукта, требуется определить количество транспортируемого продукта по каждому из участков трубопроводной системы так, чтобы количество доставленного на предприятие переработки продукта было максимальным.

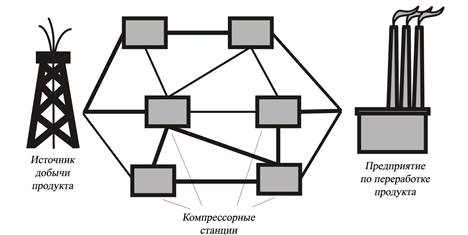
Рис. 15.1. Иллюстрация задачи о максимальном потоке в сети

Оценочной функцией в данной задаче является количество продукта, доставленного на предприятие переработки, а ограничениями служат предельные значения пропускной способности каждого участка рассматриваемой системы.

В бизнес-приложениях встречаются самые разнообразные варианты данной задачи, например, нахождение максимального пассажиропотока в транспортной системе мегаполиса, регулирование транспортных потоков на автомобильных магистралях и пр. Для наиболее эффективного анализа и решения подобных задач, их следует рассматривать в обобщенной постановке в форме задачи о максимальном потоке в сетевом графе или сети.

Чтобы в общем случае сформулировать задачу о максимальном потоке в сети, для рассматриваемой системы магистральных трубопроводов построим граф. В данном графе одна из вершин, называемая источником, будет соответствовать источнику добычи продукта, другая, называемая стоком, - предприятию по переработки этого продукта. Остальные вершины графа интерпретируются как компрессорные станции. Каждое ребро графа в этом случае будет соответствовать наличию участка трубопровода между парой компрессорных станций. Вес ребра равен пропускной способности соответствующего участка трубопровода.

Таким образом, задача о максимальном потоке в сети формулируется как задача нахождения переменных значений величин потока по каждому ребру графа, которые не превышают весов соответствующих ребер и максимизируют общий поток от источника к стоку.