Задачи линейного программирования. Оптимизация производственной программы.

Этот раздел математического программирования, посвященный описанию оптимальных решений, когда целевая функция и система ограничений линейно зависят от переменных задач.

В теории математического программирования исследуются задачи об определении максимального/минимального значения скалярной (числовой) функции F(х) многих переменных 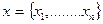при ограничивающих условиях, заданных для х.

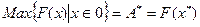или

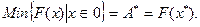
Здесь F (х) - целевая функция,{х Î 0} - ограничивающие условия, О - множество допустимых значений х. Решение задачи математического программирования дается вектором х*.

Задачи линейного программирования (ЛП) возникают, если F(х), целевая функция, является линейной, а ограничения {х Î0} удается описать в виде системы линейных уравнений и/или неравенств. Множество 0 в данном случае представляет собой выпуклый многогранник. В частном случае 0 может оказаться пустым, т.е. нет допустимых значений х. Тогда задача ЛП называетсянесовместная, т.е. не имеет решений. Запись задачи линейного программирования (ЛП)

Максимизировать (минимизировать)

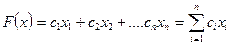
При условиях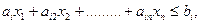

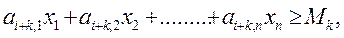
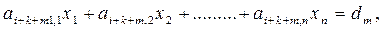
Здесь 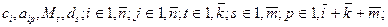постоянные, числовые коэффициенты. Смысл и значение коэффициентов c, a, b, M, d определяются той содержательной постановкой, которой отвечает данная задача ЛП.