Решение задач линейного программирования

Совместные задачи ЛП (множество 0 непустое) всегда имеют решение, хотяне обязательно единственное. Решение х* достигается на вершине многогранника О допустимых планов. На этом факте основаны все методы решения задач ЛП. Рассматриваются толькоузловые точки, лежащие на границе множества О. Они

определяются, как решения уравнений, отвечающих неравенствам. При малой размерности задачи п= 1/2/3 можно пользоваться графическим способом решения, обеспечивающим хорошую наглядность. Широко распространенным являетсясимплекс – метод.

Для применения симплекс- метода задача ЛП приводится к стандартному виду.

• все ограничения преобразуются к виду равенств с неотрицательными правыми частями (за счет введения дополнительных переменных в неравенства);

• все переменные рассматриваются как неотрицательные (за счет замены знаков коэффициентов);

• задача решается на максимум целевой функции.

Идея симплекс-метода состоит в том, что проводится последовательный перебор базовых решений (т.е. вершин многогранника 0) в сторону возрастания значения целевой функции. Алгоритм состоит в последовательном выполнении следующих шагов:

1. Выбирается начальное допустимое решение, 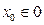Обычно начало координат, х₀(0,..,.0).

2. Рассматриваются соседние (смежные, лежащие на той же грани, что и выбранная) вершины.

3. Переходим к новой вершине, если в ней значение целевой функции больше.

4. Возврат в прежнюю вершину не возможен.

Алгоритмы симплекс- метода реализованы во многих пакетах прикладных программ. В частности в Пакете Экономических Решений (ПЭР), являющемся русифицированной версией пакета QSВ. В данном пакете приведение модели к стандартному производится автоматически.