Применение линейного программирования для экономических задач.
Термин «программирование» применяется в данном случае потому, что задачи ЛП естественно возникают при разработке планов (программ) экономической деятельности, которая всегда происходит при ограничениях. связанных, в частности, с недостатком ресурсов (неравенства £) или директивными заданиями (неравенства ³). Разработка объемных планов производства, выбор оптимальных маршрутов транспортных перевозок, распределение заданий по видам оборудования, достижение оптимальной загрузки оборудования можно проводить с помощью линейного программирования. Поэтому для переменных х используют термин «план»; «допустимый план» — план, удовлетворяющий ограничениям х Î О, «оптимальный план» х* — план, на котором целевая функция F(х) достигает своего максимума или минимума А*=F(х*). Наглядным примером является следующая модель.
Модель оптимального производственного планирования
Рассматриваются ситуации использования принципа объемного планирования. Т.е. полагается, что фиксированный период времени задан. Нужно определить какие виды продукции и в каком объеме следует производить, без детализации программы внутри периода времени. Такие задачи можно еще истолковать как задачи о распределении ресурсов.
Широкое применение принципа объемного планирования может вести к неравномерности производства и поставок части продукции в течении заданного интервала времени. Такой подход является оправданным при работе в рамках одной фирмы (микроэкономические постановки).
Содержательная постановка задачи.
Допустим, что предприятие может выпускать несколько (n) видов продукции. Для чего используется I различных ресурсов. Запасы ресурсов ограничены. Возможности дополнительной поставки не учитывается. Известны нормы затрат каждого из ресурсов на выпуск единицы продукции каждого вида. По выпуску продукции нескольких (к) видов установлены директивные задания. Нужно определить программу выпуска, обеспечивающую максимум прибыли.
Этапы формализации
1. Выбор состава плана. Всего рассматривается n видов продукции. Для их различения между собой введем номер i вида продукции, i=I,….n. Объем выпуска продукции вида i обозначим символом хi. Тогда общий план выпуска но предприятию представляет собой вектор 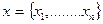 .
.
2. Учет ограничений
а. По ресурсам различных видов. Всего рассматривается I видов ресурсов. Для их различения между собой введем номер j вида ресурсов, j = I….I. Запас ресурса вида j обозначим символом bj ,j=I….I. Тогда должно быть I неравенств, отвечающих условиям по ресурсам.
б. Заданные значения экономических показателей. По k видам продукции установлен минимально допустимый объем выпуска продукции. Обозначим такой показатель через Ms . Всего задано, k значений Ms, s = I,….,k.
в. Технологические ограничения. Вообще говоря, часть продукции может быть применена в качестве полуфабриката в процессе производства, что следует учитывать при записи вида прибыли. В приведенной постановке такие условия не рассматриваются.
г. Основные экономические ограничения. Как правило, в экономических задачах все переменные полагаются неотрицательными. Объем производства хi меньше нуля быть не может.
3. Целевая функция. Согласно постановке предприятие руководствуется целью обеспечения максимума суммарной прибыли. Прибыль, получаемая в результате выпуска каждого из n видов продукции будет зависеть от уровня затрат и цены реализации. Обозначим прибыль, получаемую от реализации единицы продукции вида i символом ci xi.. Тогда прибыль, полученная от реализации всего планового объема а; продукции вида i будет ci xi . Поскольку различных видов продукции n, то в итоге получаем для прибыли значение 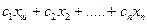
4.Формирование экономико-математической модели.Согласно постановке задачи нормы затрат каждого из I ресурсов на единицу продукции i известны. Пусть они обозначены символом aij. Тогда потребность в ресурсе j для выпуска запланированного значения хi продукции вида i будет aij хi . Суммарная потребность в ресурсе j на выполнение плана составляет 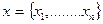 .
. 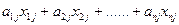
Однако известны величины bj запаса по каждому из I ресурсов. Поэтому плановая потребность 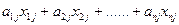 в ресурсе j не может быть больше чем bj. Следовательно, ограничениям по ресурсам отвечает I неравенств .
в ресурсе j не может быть больше чем bj. Следовательно, ограничениям по ресурсам отвечает I неравенств .
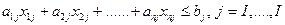
Согласно постановке задачи для k видов продукции суммарный объем выпуска не может быть меньше, чем Мt.
Допустим, что директивные задания введены для первых видов продукции. Иначе можно провести перенумерацию. Следовательно, для планового задания Xt по выпуску продукции t вводится неравенство 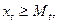 . Заметим, что условие
. Заметим, что условие 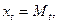 в точности отвечающее содержательной постановке, может вызвать затруднения при математическом решении ЛП, поэтому лучше рассматривать неравенство.
в точности отвечающее содержательной постановке, может вызвать затруднения при математическом решении ЛП, поэтому лучше рассматривать неравенство.
С учетом основных экономических ограничений экономико-математическая модель записывается в виде следующей задачи ЛП. Максимизировать прибыль 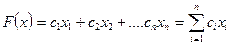 При условиях
При условиях
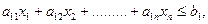
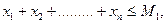
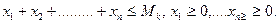
5. Решение математической задачи. Конкретные числовые значения коэффициентов вводятся в ПЭР, и производится расчет решения. Реализуется, расчет симплекс- методом.
6. Экономико-математический анализ полученных результатов.
В случае если задача ЛП не имеет решения, то это означает, что не возможно обеспечить выполнение директивных заданий при данном запасе ресурсов,
Если значение целевой функции неограниченно возрастает - то при постановке были пропущены некоторые из существенных ограничений по ресурсам, (можно делать деньги из воздуха).
Содержательная постановка задачи должна быть скорректировала. Процедура формализации повторена.
Дополнительный анализ полученного решения возможен с привлечением выдаваемых ПЭР значений двойственных переменных и данных по устойчивости решения к уточнению параметров задачи. В результате анализа после возможной корректировки и перерасчета будет получен план производства для предприятия в виде задания объема выпуска каждого из видов продукции.
Календарное планирование. Оптимизация сетевого графика
Терминкалендарное планирование (планирование оргмероприятий во времени) объединяет широкий круг задач, связанных с организацией выполнения многоэтапных крупномасштабных проектов (создание крупных объектов, проведение масштабных операций). Реализация каждого такого организационного проекта требует увязки отдельных этапов (работ) по срокам начала, продолжительности, очередности исполнения, задействованным материальным и трудовым ресурсам. Обеспечение согласованности работ между собой является цельюкалендарного планирования.
Календарное планирование применяется для планирования конкретных временных сроков запуска и выпуска продукции, нормативов длительности производственного цикла и опережений производства отдельных работ относительно выпуска головных изделий, предназначенных для реализации на соответствующем рынке продукции.
Современная методология календарного планирования предполагает привлечение представлений сетевого планирования и управления. В частности, широко применяются метод критического пути, метод оценки и пересмотра программ, известный под аббревиатурой РЕRТ – Ргоgramm Evaluation & Review Technique. Алгоритмы этих методов реализованы в пакете прикладных программ ПЭР (Пакете Экономических Решений), являющемся русифицированной версией пакета 0SВ. Примером успешного применения сетевых методов календарного планирования для обеспечения взаимосвязанных комплексов работ стали проект создания в США ракеты "Поларис" (1964) и военная операция против Ирака "Буря в пустыне" (1998).
Сетевое планирование – это одна из форм графического отражения содержания работ и продолжительности выполнения стратегических планов и долгосрочных комплексов проектных, плановых, организационных и других видов деятельности предприятия. Сетевые методы планирования находят широкое применение при разработке перспективных планов и моделей создания сложных производственных систем и других объектов долгосрочного использования.
Под сетевым планированием принято понимать графическое изображение определенного комплекса выполняемых работ, отражающее их логическую последовательность, существующую взаимосвязь и планируемую продолжительность, и обеспечивающее последующую оптимизацию разработанного графика на основе экономико-математических методов и компьютерной техники с целью его использования для текущего управления ходом работ.
Некоторые из задач, решаемых методами сетевого планирования
1.Определение общей продолжительности. Длительность выполнения проекта определяется избранной очередностью последовательно и/или параллельно исполняемых работ. Выделение работ (критических), по которым срыв сроков исполнения может привести к общей задержке проекта. Определение критического пути.
2.Анализ стоимостных характеристик. Выявление возможностей для экономии финансовых ресурсов. Ускорение выполнения проекта при максимально экономном использовании дополнительного финансирования.
3.Анализ обеспеченности ресурсами. Параллельное исполнение отдельных работ требует учета ограниченности одновременно используемых трудовых и технических ресурсов. Достаточность ресурсов для всего проекта в целом.
Основы сетевого планирования,
Математические методы, лежащие в основе сетевого планирования, опираются на понятиесетевого графика.
Сетевым графиком (или сетевой моделью) называется такое конечное множество точек(вершин) и направленных отрезков (дуг), их объединяющих, для которого:
• не существуетзамкнутой последовательности дуг в которой конечная точка предыдущей является началом последующей дуги (нет замкнутого круга);
• найдется только одна вершина(источник), в которой дуги только начинаются;
• найдется только одна вершина(сток), в которой дуги только заканчиваются;
• нельзя выделитьчасть вершин без нарушения хотя бы одной из дуг (проект не разделяется на два независимых).
• каждой из дуг приписано одно или несколько числовых значений,(длина и числовые свойства дуг).
Сетевые графики служат не только для планирования разнообразных долгосрочных работ, но и их координации между руководителями и исполнителями проектов.
Применение сетевого планирования позволяет решать следующие задачи:
1) обоснованно выбирать цели развития каждого подразделения с учетом существующих рыночных требований и планируемых конечных рез-тов
2) четко устанавливать детальные задания всем подразделениям
3) привлекать к составлению планов будущих исполнителей основных этапов работ
4) эффективно распределять ресурсы и т.д.
Для описания сетевой модели вводится нумерация вершин, i=0,…….N. Тогда каждая из работ задается парой натуральных, включая “ноль” чисел (i,j) , где i – номер начальной вершины, а j – номер конечной вершины для данной дуги.
Различных нумераций для одной и той же сетевой модели может быть достаточно много. Среди нихправильными называются те для которых начальное событие каждой работы имеет меньший номер, чем конечное. Правильность нумерации вершин сетевого графика можно обеспечить, применяя алгоритмом Фалкерсона. Пакет ПЭР работает только с правильно занумерованными сетевыми графиками.
Определение. Последовательность дуг сетевого графика, в которой конечная точка предыдущей дуги является началом последующей, называетсяпутем. Любой путь максимально возможной последовательности называется критическим.
Критических путей может быть много. Все они имеют одинаковую длину, начинаются в источнике, а заканчиваются в стоке.
Связь понятий календарного планирования и сетевых моделей.
| Календарное планирование | Сетевые модели | Значения в сетевой модели | Символ |
| проект | сетевой график | Список номеров | I=0,………,N. |
| Работа: этап проекта | дуга | пара номеров | (i,j) |
| Событие: начало (завершение) этапа | вершина | Номер | I |
| начало проекта | источник | Номер | |
| завершение проекта | сток | Номер | N |
| Продолжительность исполнения работы | длина дуги | Число | tij |
| Финансовые затраты на выполнение этапа | числовое свойство дуги | Число | cij |
| расход трудовых и технических ресурсов на выполнение этапа | числовое свойство дуги | Число | aij |
1. Задача об определении общей продолжительности исполнения проекта (метод критического пути).Пусть произвольному проекту поставлена в соответствие некоторая сетевая модель. Чтобы реализовать весь проект надо исполнить каждую из его составляющих работ. Однако некоторые из них можно выполнять параллельно, т.е. одновременно. Следовательно, общая продолжительность выполнения проекта определится самой длительной цепочкой работ, которые можно выполнять только одну за другой. Таких цепочек может быть несколько, каждой изних отвечает критический путь на сетевом графике.
Критический путь включает в себя критические события и критические работы. Термин "критическая работа" означает, что задержка выполнения каждой из таких работ неизбежно ведет к увеличению продолжительности исполнения проекта в целом, в связи с отсутствием резервов времени на этих работах. Продолжительность критического пути характеризует полное время, необходимое для выполнения всего комплекса работ. Поэтому важнейшей задачей сетевого планирования является выделение критического пути.
Предположение, Пусть сетевой график состоит из N+1 вершин с номерами i, i=0,……,N. Для каждой дуги (i,j) известна длина tij.
Чтобы выделить критический путь для каждой вершины (события) j и дуги (работы) (i,j) определяются следующие величины:
| Обозначение | Название | Смысл величины | Формула |
| ET (j) | Ранний срок наступления события j | Наименьшее время, за которое будут выполнены все взаимосвязанные работы от начала проекта (источника) до события j | ET (0) = maxi{ET(i) + tij} I=0,……..,N-1 |
| LT (j) | Поздний срок наступления события j | Длина самого короткого пути от события j до стока | ET (N) = LT(N) mink{LT(k) + tik K=0,……..,N-1 |
Вершины критического пути определяются следующим условием
ET (0) =0, ET9i)=LT(i), i=0,……..,N.
Продолжительность критического пути совпадает с полным временем выполнения проекта. Поэтому, если критический путь выделен, то можно оптимизировать время, требуемое на исполнение всех работ. Возможны следующие два подхода:
1) Для ускорения исполнения проекта в целом надо сократить продолжительности всех критических путей. Например, за счет перераспределения ресурсов между критическими и некритическими работами.
2) Изменение структуры сетевой модели для перехода последовательного выполнения работ в параллельное.
По результатам анализа и пересмотра сетевого графика проводится повторный расчет продолжительности исполнения работ. В случае, если его результат удовлетворителен, составляется директивный план-график (привязанный к календарным датам).
2. Анализ стоимостных характеристик.Рассматриваются затраты, зависящие от времени выполнения работы (связаны с рабочей силой, тепло/энергоснабжением и т.п.). Целью может быть выявление возможностей для экономии финансовых ресурсов, либо ускорение выполнения проекта при максимально экономном использовании дополнительного финансирования,
Для анализа стоимостных характеристик выполнения проекта нужно определить финансовые затраты на выполнение каждого из этапов проекта. Сделаем некоторые предположения.
Предположение. Пусть определен сетевой график.
1. Для каждой из работ (i,j) заданы числовые значения:
| Обозначения | Термин | Смысл | Соотношения |
| t1ij | нормальное время выполнения работы | Работа (i,j) будет сделана за это время в нормальном режиме (без дополнительного финансирования) | t1ij>0 |
| С1ij | Нормальная стоимость выполнения работы | Столько стоит сделать работу (i,j) за время t1ij | С1ij >0 |
| t0ij | Минимальная продолжительность выполнения работы | Быстрее чем за это время работу (i,j) cделать нельзя | t1ij >t0ij>0 |
| С0ij | Минимальная стоимость выполнения работы | Столько нужно заплатить, чтобы сделать работу (1,1) за минимальное время | С0ij >С1ij |
2. Затраты на каждую работу (i,j) целиком определяются длительностью ее выполнения.
3. Зависимость затрат С от времени t можно приближенно описать линейной функцией. Предположение 3 означает, что вообще говоря график зависимости стоимости от времени не является прямой линией (См. Рис.) Однако для наших целей достаточно положить, что за выполнение работы (i,j) в течении времени t нужно заплатить С, C= -Сij (t- t0ij)
где 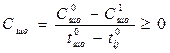 .Коэффициент Сij характеризует увеличение стоимости выполнения работы (i,j) при уменьшении продолжительности на единицу времени.
.Коэффициент Сij характеризует увеличение стоимости выполнения работы (i,j) при уменьшении продолжительности на единицу времени.

Рис. График зависимости стоимости от времени выполнения работы
Таким образом, оптимизация стоимостных характеристик сетевой модели может осуществляться в двух вариантах: 1) Сокращение продолжительности выполнения проекта за счет максимально экономного дополнительного финансирования.Продолжительность исполнения проекта равна длине критического пути. Поэтому в анализе участвуют только работы входящие в критический путь. Анализ проводится по шагам. Для каждой из работ, входящих в критический путь. определяется стоимостной коэффициент Сij. Затем сокращаются на единицу те критические работы, для которых этот коэффициент минимален. После чего проверяется не появилось ли новых критических путей. Шаги повторяются, пока хватает денег, или длина каждой из работ не становится минимально возможной. 2) Экономия финансовых ресурсов. Если продолжительность выполнения проекта задана, то можно сберечь деньги, выполняя некритические работы медленнее. Замедляются те из некритических работ, для которых значения коэффициента Сij самые большие.
3. Анализ обеспеченности ресурсами.  По перечню работ дается привязка к ранним срокам начала работ. В результате составляется план-график обеспеченности ресурсами. (См. Рис.)
По перечню работ дается привязка к ранним срокам начала работ. В результате составляется план-график обеспеченности ресурсами. (См. Рис.)
Рис. График анализа обеспеченности ресурсами
Оптимизация сетевых графиков заключается в улучшении процессов планирования, организации и управления комплексом работ с целью сокращения расходования экономических ресурсов. И повышения финансовых результатов при заданных плановых ограничениях. Оптимизация сетевых графиков подразделяется на частную и комплексную. Основными видами частной оптимизации являются два известных экономических подхода: 1) минимизация времени выполнения комплекса планируемых работ при заданной стоимости проекта; 2) минимизация стоимости всего комплекса работ при заданном времени выполнения проекта.Комплексная оптимизация сетевых моделей состоит в нахождении наилучших соотношений показателей затрат экономических ресурсов и сроков выполнения планируемых работ применительно к определенным производственным условиям.
Дата добавления: 2015-07-30; просмотров: 1632;
