Деякі визначення
Нехай G - неорієнтований граф.
Визначення. Маршрутом в G називається скінченна або нескінченна послідовність ребер S = {…, e0, e1, …, en, …} в якій кожні два сусідні ребра ei - 1 і ei мають спільну вершину, тобто
e0 = (v0, v1)
e1 = (v1, v2)
e2 = (v2, v3)
. . .
en = (vn, vn + 1).
Визначення. Якщо в S немає ребер, які стоять перед e0, то v0 називається початковою вершиною S; якщо немає ребер після en - 1, то vn - кінцевою вершиною. Якщо вершина vi належить і ei - 1 і ei, то вона називається внутрішньою.
Визначення. Якщо маршрут S має початкову і кінцеву вершини, то він називається скінченним; якщо S має початок і не має кінцевої вершини (або навпаки), то він називається односторонньо-нескінченним; якщо немає ні початкової вершини ні кінцевої – то двосторонньо-нескінченними. Якщо S має початкову вершину v0 і кінцеву vn, то позначається
S = S(v0, vn)
(тобто S - це маршрут довжини n, який з’єднує вершини v0 і vn ).
Визначення. Якщо v0 = vn, то маршрут називається циклічним.
Визначення. Якщо vi і vj - дві вершини маршруту S, то
S(vi, vj) = (ei, …, ei + 1, …, ej - 1)
називається підмаршрутом.
На рис.5 маршрут S = (e1, e2, e3, e4, e5) є скінченним, має довжину 5, початкову вершину v1 і кінцеву v5. Маршрут S = (e2, e3, e4) є підмаршрутом даного маршруту.
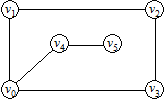
Рис.5
Визначення. Ланцюг – це маршрут, кожне ребро якого зустрічається рівно один раз. Циклічний ланцюг називається циклом.
Визначення. Нециклічний ланцюг називається простим, якщо в ньому жодна вершина не повторюється. Цикл з початком (і кінцем) в v0 називається простим, якщо в ньому жодна вершина, крім v0 не повторюється.
Зрозуміло, що частина ланцюга або циклу теж є ланцюгом або циклом.
Для орієнтованих графів вводяться в розгляд як неорієнтовані маршрути (ланцюги) (тобто не приймається до уваги орієнтація ребер), так і орієнтовані маршрути (ланцюги).
Дата добавления: 2015-08-26; просмотров: 763;
