Расстояние от точки до прямой

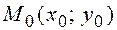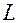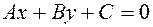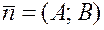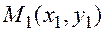Выразим расстояние от произвольной точки на плоскости до прямой : . Пусть нам известны и лежащая на прямой. Тогда, расстояние от точки до прямой можно выразить через проекцию 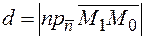. И по формуле определяем: .

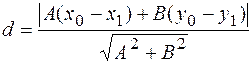Раскрывая скобки получим:

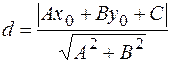(8..3)

Если дано нормированное уравнение прямой, то .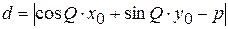

Определение. Если в пространстве задана произвольная плоскость 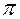и фиксирована произвольная декартова система координат, то плоскость 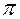определяется в этой системе координат уравнением первой степени (и наоборот: всякое уравнение первой степени с тремя неизвестными 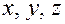определяет плоскость относительно данной системы координат).