Условия параллельности и ортогональности прямых, угол между прямыми, пучок прямых. Уравнения плоскости в пространстве.
Цель: Изучить условия расположения прямых на плоскости, метод вычисления угла между прямыми. Изучить уравнения плоскости в пространстве и основные характеристики.
Расположение прямых на плоскости определяется по взаимному расположению их направляющих векторов или отношением угловых коэффициентов.
1. Пусть прямые заданы в общем виде. 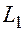 :
: 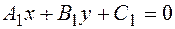 и
и 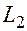 :
: 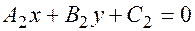 , где
, где 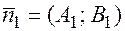 ,
, 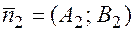 соответствующие им векторы нормали.
соответствующие им векторы нормали.
Если 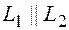 , то
, то 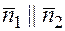 и координаты векторов пропорциональны
и координаты векторов пропорциональны 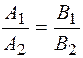 .
.
Если 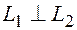 , то
, то 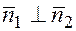 и значит, скалярное произведение векторов равно нулю
и значит, скалярное произведение векторов равно нулю 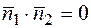 . В координатной форме это запишется как
. В координатной форме это запишется как 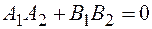 .
.
Если 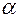 - угол между прямыми
- угол между прямыми 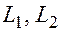 , то он равен углу между векторами
, то он равен углу между векторами 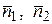 и тогда
и тогда
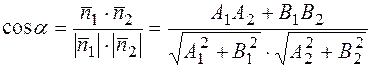 .
.
2. Пусть прямые заданы каноническим уравнением. 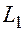 :
: 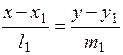 и
и 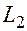 :
: 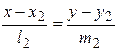 , где
, где 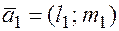 ,
, 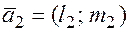 соответствующие им направляющие векторы.
соответствующие им направляющие векторы.
Если 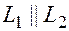 , то
, то 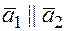 и их соответствующие координаты пропорциональны
и их соответствующие координаты пропорциональны 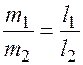 .
.
Если 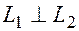 , то
, то 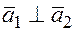 и их скалярное произведение равно нулю
и их скалярное произведение равно нулю 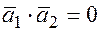 . В координатной форм
. В координатной форм 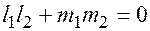 .
.
Если 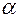 - угол между прямыми
- угол между прямыми 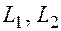 то он равен углу между векторами
то он равен углу между векторами 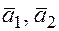 и тогда
и тогда
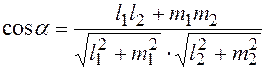 .
.
3. Пусть уравнения прямых заданы через угловой коэффициент. 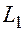 :
: 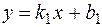 и
и 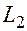 :
: 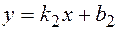 (или в виде (7.7)). Тогда угол между прямыми, определяется как разность углов наклона прямых к положительному направлению оси
(или в виде (7.7)). Тогда угол между прямыми, определяется как разность углов наклона прямых к положительному направлению оси 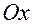 :
: 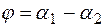 подставляя это в формулу тангенса разности, получим:
подставляя это в формулу тангенса разности, получим:
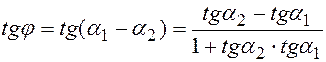 (8.1)
(8.1)
Или через угловые коэффициенты прямых
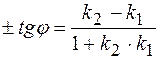 (8.2)
(8.2)
Из соотношения (7.9) легко определяются условия ортогональности и коллинеарности прямых.
Если 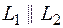 , то угол между ними равен нулю
, то угол между ними равен нулю 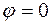 и, следовательно
и, следовательно 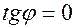 , что возможно только при обращении в нуль числителя в формуле (7.9)
, что возможно только при обращении в нуль числителя в формуле (7.9) 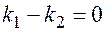 и значит, для параллельных прямых
и значит, для параллельных прямых 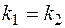 .
.
Если 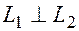 , то
, то 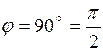 , и следовательно
, и следовательно 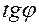 не определен, т.е. знаменатель формулы (7.9) обращается в нуль :
не определен, т.е. знаменатель формулы (7.9) обращается в нуль : 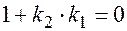 . Откуда получаем условие ортогональности прямых:
. Откуда получаем условие ортогональности прямых: 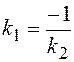 .
.
Дата добавления: 2015-08-26; просмотров: 1035;
