Уравнение плоскости проходящей через точку и вектор нормали

Определение: Всякий ненулевой вектор 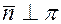ортогональный плоскости, с координатами 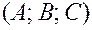, называется нормалью к плоскости.

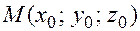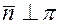Пусть на плоскости задана некоторая точка и вектор нормали . Если вектор , то 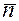ортогонален любой прямой этой плоскости (рис. 8.1), следовательно, 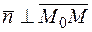, тогда их скалярное произведение обращается в ноль 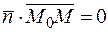. Записывая последнее равенство в координатной форме получим:

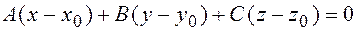(8.4)

где .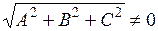

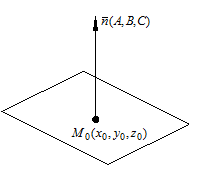
Рис. 8.1.