Нормированное уравнение прямой
Пусть 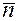 - единичная нормаль заданной прямой , т.е.
- единичная нормаль заданной прямой , т.е. 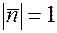 . Возьмем на прямой произвольную точку
. Возьмем на прямой произвольную точку 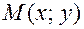 , координаты ее радиус вектора совпадают с координатами точки. Выразим уравнение прямой
, координаты ее радиус вектора совпадают с координатами точки. Выразим уравнение прямой 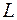 через угол
через угол 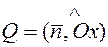 и радиус вектор
и радиус вектор 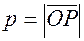 (рис. 7.5). Т.к.
(рис. 7.5). Т.к. 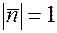 , то его координатами являются направляющие косинусы
, то его координатами являются направляющие косинусы 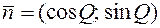 . Т.к.
. Т.к. 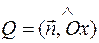 и
и 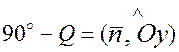 , то
, то  , и следовательно
, и следовательно 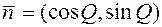 .
.
Точка 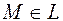 , ее проекция на вектор нормали равна радиус вектору
, ее проекция на вектор нормали равна радиус вектору 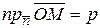 . Но, проекцию точки на вектор можно вычислить через скалярное произведение (формула 5.7)
. Но, проекцию точки на вектор можно вычислить через скалярное произведение (формула 5.7) 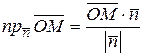 . Приравнивая правые части и учитывая, что
. Приравнивая правые части и учитывая, что 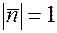 получим
получим 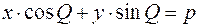 .
.
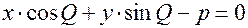 (7.10)
(7.10)
– нормированное уравнение прямой.

Рис. 7.5
Установим связь между нормированным и общим уравнением прямой.
Если дано 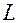 :
: 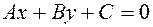 , то
, то 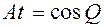 ,
, 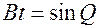 ,
, 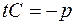 .
. 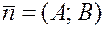 , поэтому
, поэтому 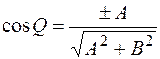 ,
, 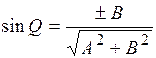 ,
, 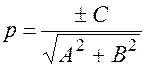 , где знак выражения зависит от
, где знак выражения зависит от 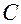 (противоположный
(противоположный 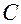 ), следовательно, получается нормированное уравнение
), следовательно, получается нормированное уравнение 
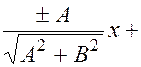
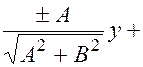
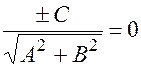
Определение. Совокупность лежащих на данной плоскости 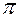 прямых, проходящих через точку
прямых, проходящих через точку 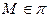 , называют пучком прямых с центром в точке
, называют пучком прямых с центром в точке  .
.
Теорема. Если  и
и 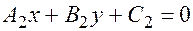 уравнения двух различных прямых, пресекающихся в некоторой точке
уравнения двух различных прямых, пресекающихся в некоторой точке  , а
, а 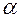 и
и  произвольные числа, причем
произвольные числа, причем 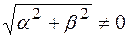 , тогда
, тогда  есть уравнение прямой, проходящей через точку
есть уравнение прямой, проходящей через точку  . Более того, какова бы ни была наперед заданная проходящая через точку
. Более того, какова бы ни была наперед заданная проходящая через точку  прямая, она определяется выше записанным уравнением при некоторых
прямая, она определяется выше записанным уравнением при некоторых 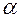 и
и  .
.
Дата добавления: 2015-08-26; просмотров: 1357;
