Уравнение плоскости, проходящей через три различные точки

Даны три точки: , , .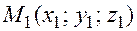

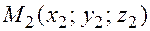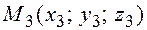Чтобы произвольная точка пространства 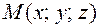принадлежала плоскости, т.е. 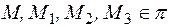, необходимо и достаточно, чтобы

Рис. 8.3

векторы 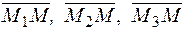были компланарны (рис. 8.3), следовательно, смешанное произведение векторов должно равняться нулю 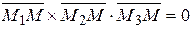. Записывая данное равенство в координатной форме получим уравнение плоскости проходящей через три точки:

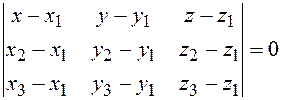(8.7)