Нормированное уравнение плоскости
Пусть дана 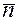 – единичная нормаль и расстояние от точки
– единичная нормаль и расстояние от точки 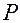 до начала координат
до начала координат  , выразим уравнение плоскости
, выразим уравнение плоскости 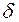 через:
через: 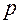 и углы
и углы 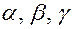 между осями и вектором
между осями и вектором 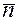 (рис. 8.5).
(рис. 8.5).

Рис. 8.5
Координаты вектора 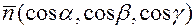 , очевидно
, очевидно 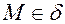 тогда и только тогда, когда
тогда и только тогда, когда 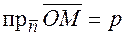 , следовательно, должно выполняться равенство
, следовательно, должно выполняться равенство 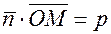 , отсюда получаем нормированное уравнение плоскости
, отсюда получаем нормированное уравнение плоскости 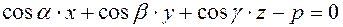 .
.
Чтобы привести полное уравнение 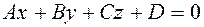 к нормированному виду, нужно каждый коэффициент уравнения умножить на нормирующий множитель
к нормированному виду, нужно каждый коэффициент уравнения умножить на нормирующий множитель 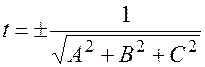 , знак зависит от
, знак зависит от 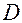 . Знак выбираем противоположный
. Знак выбираем противоположный 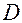 , т. к.
, т. к. 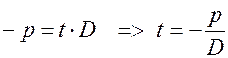 .
.
Расстояние от произвольной точки пространства до указанной плоскости определяется аналогично расстоянию от точки до прямой :
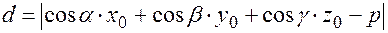 (8.9)
(8.9)
Определение.Совокупность всех плоскостей, проходящих через одну и ту же прямую L, называется пучком плоскостей (с центром в L).
Теорема. Если даны две не параллельные плоскости 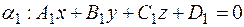 ,
, 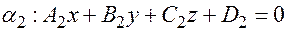 и
и 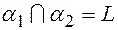 , а
, а 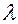 и
и 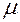 – какие угодно числа неравные нулю одновременно, то
– какие угодно числа неравные нулю одновременно, то 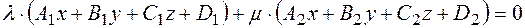
есть уравнение плоскости, проходящей через прямую L.
Определение.Совокупность всех плоскостей, проходящих через данную точку 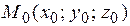 , называется связкой плоскостей (с центром в
, называется связкой плоскостей (с центром в 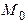 ).
).
Теорема. Уравнение связки с центром в 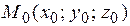 имеет вид
имеет вид 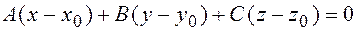 , где
, где 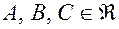 и не равны нулю одновременно.
и не равны нулю одновременно.
Дата добавления: 2015-08-26; просмотров: 1125;
