Каноническое уравнение прямой
Ненулевой вектор 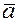 параллельный заданной прямой
параллельный заданной прямой 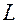 будем называть направляющим вектором этой прямой (рис. 9.2). Выведем уравнение прямой, проходящей через заданную точку
будем называть направляющим вектором этой прямой (рис. 9.2). Выведем уравнение прямой, проходящей через заданную точку 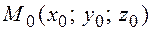 и имеющей заданный направляющий вектор
и имеющей заданный направляющий вектор 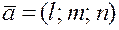 .
.
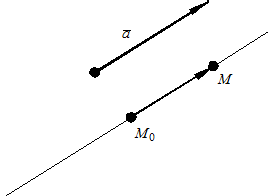
Рис. 9.2
Возьмем произвольную точку пространства 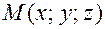 лежащую на прямой
лежащую на прямой 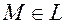 , построенный на точках вектор
, построенный на точках вектор 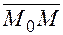 будет параллелен направляющему вектору
будет параллелен направляющему вектору 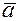 . В координатной форме это условие запишется:
. В координатной форме это условие запишется:
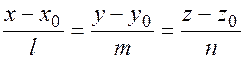 (9.2)
(9.2)
Уравнение принято называть каноническим уравнением прямой в пространстве.
Задача. Как от уравнения вида (9.1) перейти к уравнению вида (9.2).
Достаточно найти: 1) хотя бы одну точку 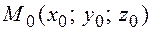 , решая систему уравнений (9.1);
, решая систему уравнений (9.1);
2) т. к. 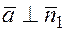 и
и 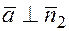 , можно найти
, можно найти 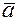 , воспользовавшись свойством векторного произведения:
, воспользовавшись свойством векторного произведения: 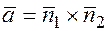 .
.
Дата добавления: 2015-08-26; просмотров: 650;
