Уравнение плоскости через точки и направляющие вектора
Определение: Два произвольных неколлинеарных вектора, лежащих в указанной плоскости или параллельных ей, называются направляющими векторами данной плоскости.
Для того, чтобы записать уравнение плоскости, проходящей через заданную точку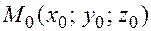 
и два направляющих вектора плоскости 
, 
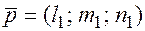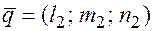воспользуемся условием компланарности векторов 
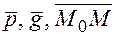(рис.8.4), где 
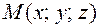произвольна точка пространства принадлежащая плоскости.
Рис.8.4
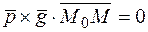или в координатной форме:
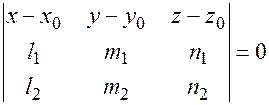(8.8)
Дата добавления: 2015-08-26; просмотров: 2816;