Дифференцирующее звено

Различают идеальное и реальное дифференцирующие звенья. Уравнение динамики идеального звена:

y(t) = 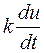, или y = kpu.

Здесь выходная величина пропорциональна скорости изменения входной величины. Передаточная функция:

W(p) = kp.

При k=1 звено осуществляет чистое дифференцирование W(p) = p. Переходная характеристика:

h(t) = k 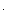1'(t) = d(t).

Идеальное дифференцирующее звено реализовать невозможно, так как величина всплеска выходной величины при подаче на вход единичного ступенчатого воздействия всегда ограничена. На практике используют реальные дифференцирующие звенья, осуществляющие приближенное дифференцирование входного сигнала.

Его уравнение:

T p y + y = k T p u.

Передаточная функция:

W(p) = .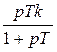

При малых Т звено можно рассматривать как идеальное дифференцирующее. Переходную характеристику можно вывести с помощью формулы Хевисайда:

,

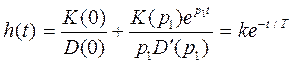здесь p₁=-1/T - корень характеристического уравнения D(p) = Tp + 1 = 0; кроме того, D'(p₁) = T.

По переходной характеристике, имеющей вид экспоненты (рис.4.8а), можно определить передаточный коэффициент k и постоянную времени Т. Примерами таких звеньев могут являться четырехполюсник из сопротивления и емкости (рис.4.8б) и демпфер, (рис.4.8.в). Дифференцирующие звенья являются главным средством, применяемым для улучшения динамических свойств САУ.

При подаче на вход единичного ступенчатого воздействия выход оказывается ограничен по величине и растянут во времени (рис.4.8а).

Рисунок 4.8 – Разновидность типовых дифференцирующих звеньев САР.