Понятие частотных характеристик

В условиях реальной эксплуатации САР часто возникает необходимость определить реакцию на периодические сигналы, т.е. определить сигнал на выходе САР, если на один из входов подается периодически сигнал гармонической формы. Решение этой задачи возможно получить путем использования частотных характеристик системы.

Зависимости, связывающие амплитуду и фазу выходного сигнала с частотой входного сигнала, называются частотными характеристиками (ЧХ). Анализ ЧХ системы с целью исследования ее динамических свойств называется частотным анализом.

Частотные характеристики могут быть получены экспериментальным или аналитическим путем. При аналитическом определении исходным моментом является одна из передаточных функций САР (по управлению или по возмущению).

Возможно также определение частотных характеристик исходя из передаточных функций разомкнутой системы и передаточной функции по ошибке.

Если подать на вход системы с передаточной функцией W(p) гармонический сигнал

u(t)= U_m(cos t + j sin ωt),

где U_m – амплитуда колебаний, ω – частота колебаний, t – время, то после завершения переходного процесса на выходе установятся гармонические колебания

y(t) =Y_me^j(ωt+φ) = Y_m e^jωt e^jφ

с той же частотой ω, но иными амплитудой Y_m и фазой φ, зависящими от частоты ω возмущающего воздействия. По ним можно судить о динамических свойствах системы.

Подставим выражения для u(t) и y(t) в уравнение динамики

(a_оpⁿ + a₁p^{n - 1} + a₂p^{n - 2} + ... + a_n)y = (b_оp^m + b₁p^m-1 + ... + b_m )u.

Учтем, что

,

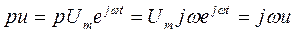а значит pⁿu = pⁿU_me^jωt = U_m (jω)ⁿ e^jωt = (jω)ⁿu.

Аналогичные соотношения можно записать и для левой части уравнения. Получим:

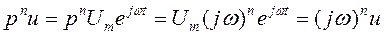
По аналогии с передаточной функцией можно записать:

.

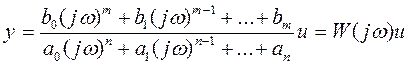W(jω), равная отношению выходного сигнала к входному при изменении входного сигнала по гармоническому закону, называется частотной передаточной функцией. Легко заметить, что она может быть получена путем простой замены p на jω в выражении W(p).

W(jω) есть комплексная функция, поэтому:

;

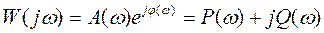где P(ω) - вещественная ЧХ (ВЧХ);

Q(ω) - мнимая часть ЧХ (МЧХ);

А(ω) - амплитудная ЧХ (АЧХ);

φ (ω) - фазовая ЧХ (ФЧХ).

АЧХ дает отношение амплитуд выходного и входного сигналов, ФЧХ - сдвиг по фазе выходной величины относительно входной:

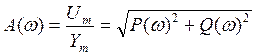
Если W(jω) изобразить вектором на комплексной плоскости, то при изменении

и ω от 0 до + его конец будет вычерчивать кривую, называемую годографом вектора W(j ω), или амплитудно - фазовую частотную характеристику (АФЧХ) (рис.5.1.). Ветвь АФЧХ при изменении ω от - до 0 можно получить зеркальным отображением данной кривой относительно вещественной оси.

Рисунок 5.1 – Годограф вектора W(j ω) (АФЧХ).

В ТАУ широко используются логарифмические частотные характеристики (ЛЧХ) (рис.5.2.): логарифмическая амплитудная ЧХ (ЛАЧХ) L(ω) и логарифмическая фазовая ЧХ (ЛФЧХ) φ(ω). Они получаются путем логарифмирования передаточной функции.

По оси абсцисс откладывается частота ω в логарифмическом масштабе. То есть единичным промежуткам по оси абсцисс соответствует изменение ω в 10 раз. Такой интервал называется декадой. Так как lg(0) = - 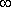, то ось ординат проводят произвольно.

Рисунок 5.2 – Логарифмические частотные характеристики.