Интегрирующее звено

Передаточная функция: W(p) = k/p.

Рассмотрим частный случай, когда k = 1, то есть W(p) = 1/p.

АФЧХ: W(j ω) = .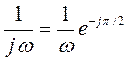

ВЧХ: P(ω) = 0.

МЧХ: Q(ω) = - 1/ ω.

АЧХ: A(ω) = 1/ ω.

ФЧХ: φ( ω) = - π/2.

ЛАЧХ: L(ω) = 20lg(1/ ω) = - 20lg(ω).

ЧХ показаны на рис.5.4. Все частоты звено пропускает с запаздыванием по фазе на φ=90^о. Амплитуда выходного сигнала увеличивается при уменьшении частоты и уменьшается до нуля при росте частоты (звено "заваливает" высокие частоты).

ЛАЧХ представляет собой прямую, проходящую через точку L(ω) = 0 при ω = 1. При увеличении частоты на декаду ордината уменьшается на 20lg10 = 20дб, то есть наклон ЛАЧХ равен - 20 дб/дек (децибел на декаду).

Рисунок 5.4 – Частотные характеристики интегрирующего звена.

5.2.3. Апериодическое звено

Для апериодического звена при k = 1 получаем следующие выражения ЧХ.

Передаточная функция:

;

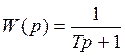АФЧХ: ;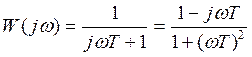

ВЧХ: ;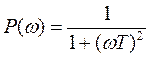

МЧХ: .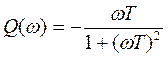

Рисунок 5.5 – Частотные характеристики для апериодического звена.

(ω) = φ₁ - φ₂ = - arctg(ω T);

;

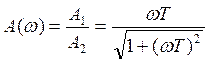L(ω) = 20lg(A(ω)) = - 10lg(1 + (ω T)²),

где: A₁ и A₂ - амплитуды числителя и знаменателя ЛФЧХ;

φ ₁ и φ ₂ - аргументы числителя и знаменателя.

Частотные характеристики показаны на рис.5.5. АФЧХ есть полуокружность радиусом 1/2 с центром в точке P = 1/2.

При построении асимптотической ЛАЧХ считают, что при ω < ω₁ = 1/T можно пренебречь компонентой (ωT)² в выражении для L(ω), то есть L(ω) 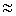- 10lg1 = 0. При ω > ω ₁ пренебрегают единицей в выражении в скобках, то есть L(ω) 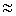- 20lg(ω).

Поэтому ЛАЧХ проходит вдоль оси абсцисс до сопрягающей частоты, затем - под наклоном - 20 дб/дек. Частота ω₁ называется сопрягающей частотой. Максимальное отличие реальных ЛАЧХ от асимптотических не превышает 3 дб при ω = ω₁.

ЛФЧХ асимптотически стремится к нулю при уменьшении ω до нуля (чем меньше частота, тем меньше искажения сигнала по фазе) и k- /2 при возрастании ω до бесконечности. Перегиб в точке ω = ω₁ при φ(ω) = - /4. ЛФЧХ всех апериодических звеньев имеют одинаковую форму и могут быть построены по типовой кривой с параллельным сдвигом вдоль оси частот.

5.2.4. Правила построения ЧХ элементарных звеньев

При построении ЧХ некоторых звеньев можно использовать “правило зеркала”: при k=1 ЛАЧХ и ЛФЧХ звеньев с обратными передаточными функциями зеркальны относительно горизонтальной оси. Так, на рис.5.6 изображены ЧХ идеального дифференцирующего (а) и идеального форсирующего звеньев (б).

Если k ≠ 1, то передаточную функцию звена можно рассматривать как произведение W = kW₁,

где W₁ - передаточная функция с k = 1.

При этом амплитуда вектора АФЧХ W(jω) при всех значениях φ должна быть увеличена в k раз, то есть A(ω) = kA₁(ω).

Центр полуокружности АФЧХ апериодического звена будет находиться не в точке P = 1/2, а в точке k/2. ЛАЧХ также изменится: L(ω) = 20lgA(ω) = 20lgkA₁(ω) = 20lgk + 20lgA₁(ω).

При k ≠ 1 ЛАЧХ звена нужно поднять по оси ординат, не меняя ее формы, на 20lg k. На ЛФЧХ изменение k никак не отразится. Для примера на рис.5.7 приведены частотные характеристики апериодического звена при k = 10 и T = 1c. При этом ЛАЧХ апериодического звена с k = 1 поднята вверх на 20lg 10 = 20.

Рисунок 5.6 – ЧХ идеального дифференцирующего (а) и идеального

форсирующего звеньев (б).

Рисунок 5.7 – Частотные характеристики апериодического звена

при k = 10 и T = 1c.