Апериодическое звено
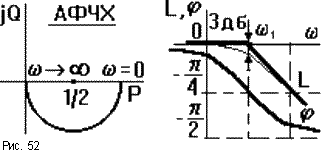
При k = 1 получаем следующие выражения ЧХ:
W(p) = 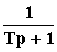 ;
;
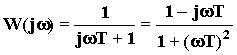 ;
;
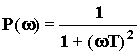 ;
;
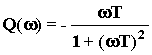 ;
;
 (
(  ) =
) =  1 -
1 -  2 = - arctg(
2 = - arctg(  T);
T);
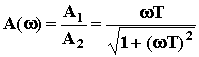 ;
;
L(  ) = 20lg(A(
) = 20lg(A(  )) = - 10lg(1 + (
)) = - 10lg(1 + (  T)2).
T)2).
Здесь A1 и A2 - амплитуды числителя и знаменателя ЛФЧХ;  1 и
1 и  2 - аргументы числителя и знаменателя. ЛФЧХ:
2 - аргументы числителя и знаменателя. ЛФЧХ:
ЧХ показаны на рис.52. АФЧХ есть полуокружность радиусом 1/2 с центром в точке P = 1/2. При построении асимптотической ЛАЧХ считают, что при  <
<  1 = 1/T можно пренебречь (
1 = 1/T можно пренебречь (  T)2 выражении для L(
T)2 выражении для L(  ), то есть L(
), то есть L(  )
)  - 10lg1 = 0.. При
- 10lg1 = 0.. При  >
>  1 пренебрегают единицей в выражении в скобках, то есть L(w)
1 пренебрегают единицей в выражении в скобках, то есть L(w)  - 20lg(wT). Поэтому ЛАЧХ проходит вдоль оси абсцисс до сопрягающей частоты, затем - под наклоном - 20 дб/дек. Частота w1 называется сопрягающей частотой. Максимальное отличие реальных ЛАЧХ от асимптотических не превышает 3 дб при
- 20lg(wT). Поэтому ЛАЧХ проходит вдоль оси абсцисс до сопрягающей частоты, затем - под наклоном - 20 дб/дек. Частота w1 называется сопрягающей частотой. Максимальное отличие реальных ЛАЧХ от асимптотических не превышает 3 дб при  =
=  1.
1.
ЛФЧХ асимптотически стремится к нулю при уменьшении w до нуля (чем меньше частота, тем меньше искажения сигнала по фазе) и к -  /2 при возрастании
/2 при возрастании  до бесконечности. Перегиб в точке
до бесконечности. Перегиб в точке  =
=  1 при
1 при  (
(  ) = -
) = -  /4. ЛФЧХ всех апериодических звеньев имеют одинаковую форму и могут быть построены по типовой кривой с параллельным сдвигом вдоль оси частот.
/4. ЛФЧХ всех апериодических звеньев имеют одинаковую форму и могут быть построены по типовой кривой с параллельным сдвигом вдоль оси частот.
Дата добавления: 2015-07-24; просмотров: 973;
