Инерционное звено первого порядка (апериодическое)

Уравнение динамики инерционного звена первого порядка:

,

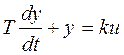или

Tpy + y = ku.

Это уравнение динамики, называемое иногда кривой разгона, имеет вид экспоненты.

Передаточная функция:

W(p) = .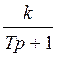

Переходная характеристика может быть получена с помощью формулы Хевисайда:

,

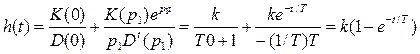где p₁ = - 1/T - корень уравнения D(p) = Tp + 1 = 0; D'(p₁) = T.

Переходная характеристика имеет вид экспоненты (рис.4.5а), по которой можно определить передаточный коэффициент k, равный установившемуся значению h(ассимтота), и постоянную времени Т_о по времени t, соответствующему точке пересечения касательной к кривой в начале координат с ее асимптотой. При достаточно больших Т_о звено на начальном участке может рассматриваться как интегрирующее, при малых Т звено приближенно можно рассматривать как безынерционное.

Пример апериодического звена - четырехполюсник из сопротивления R и емкости C (рис.4.5б).

Рисунок 4.5 – Инерционное звено первого порядка (апериодическое).

У экспоненты есть свойство: если к любой ее точке провести касательную, а затем точку касания и точку пересечения касательной с асимптотой, к которой с течением времени приближается экспонента, спроецировать на ось времени t, то получают одну и ту же величину времени - «постоянную времени» Т_о, которая характеризует инерционные свойства объекта.

Ордината асимптоты, к которой стремится экспонента, по величине равна коэффициенту k в передаточной функции апериодического звена. Таким образом, по графику кривой разгона можно найти оба коэффициента- k и Т_о в передаточной функции апериодического звена.

Еще одним примером реализации апериодического звена может быть установка - емкость равного по высоте сечения, которая изображена на рис. 4.6. Бак на входе заполняет поток воды с расходом Q₁, из бака вытекает свободно поток с расходом Q₂.

Рисунок 4.6 – Пример реализации апериодического звена при наполнении и истечении емкости с равным расходом.

Регулируемый параметр Х_вых - уровень Н в баке. При «единичном скачке» Q₁ уровень Н повышается, увеличивается гидростатическое давление, возрастает Q₂ и затем уровень Н стабилизируется (экспонента приближается к асимптоте). Эта способность самостоятельно восстанавливать равновесие, присущая объектам, аппроксимируемым апериодическим ТДЗ за счет наполнения или опорожнения энергии или вещества, называется самовыравниванием.

Самовыравнивание количественно определяется коэффициентом самовыравнивания, который равен обратной величине коэффициента k передаточной функции звена:

С= 1/ k.