Доказательство. Докажем методом математической индукции в І форме для натуральных чисел по , что является отображением.

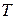- бинарная операция (?)

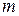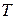Докажем методом математической индукции в І форме для натуральных чисел по , что является отображением.

База индукци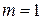и :

и 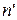определено и однозначно, поскольку 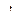- отображение.

Индуктивное предположение :

Пусть определено и однозначно.

Покажем справедливость утверждения для :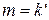

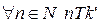определено и однозначно (?)

. Поскольку определено и однозначно, а 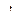- отображение, 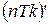также определено и однозначно.

Также методом математической индукции в І форме для натуральных чисел по 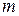устанавливает существование и единственность операции .

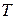Операция 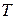единственна (?)

Предположим, что наряду с операцией 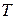существует операция 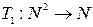, удовлетворяющая аксиомам сложения:

1. ;

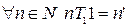2. .

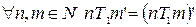База индукции :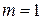

.

Индуктивное предположение :

Пусть .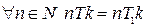

Покажем справедливость утверждения для :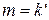

(?)

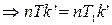, что противоречит предположению.

Таким образом, , следовательно, .

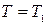Операция 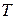существует (?)

Рассмотрим систему множеств 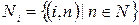, где 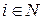. Индукцией по 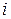докажем, что существует отображение 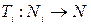, удовлетворяющее следующим условиям:

1. ;

2. .

База индукции :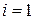

Определим по правилу:

.

Очевидно, что таким образом определенное существует, причем

1. ;

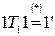2. .

Индуктивное предположение :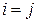

Пусть 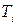существует и удовлетворяет условиям:

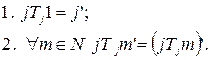
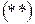
Покажем справедливость утверждения для :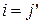

(?)

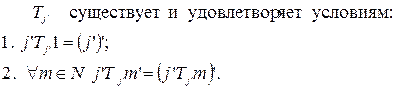Определим 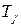по правилу:

.

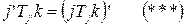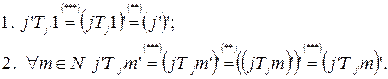
Определим операцию 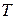по правилу . Доказано, что 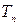существует и удовлетворяет аксиомам сложения, следовательно, существует и отображение 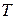, удовлетворяющее аксиомам сложения.

что и требовалось доказать.

Замечание. Поскольку операция 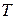, удовлетворяющая аксиомам сложения, единственна на множестве натуральных чисел, для нее введем специальный символ +, т.е. .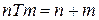

Свойства операции сложения на множестве натуральных чисел:

1) .