Доказательство. Рассмотрим две произвольные модели и

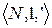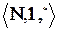Рассмотрим две произвольные модели и . Пусть соответствие 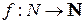задано по следующим правилам:

1. ;

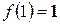2. .

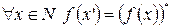Покажем, что 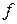является биекцией. Тем самым и докажем изоморфизм моделей.

Всюду определенность (?)

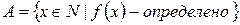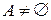. , т.к. 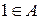. Покажем, что 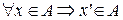. . 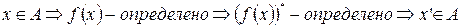Тогда, по 3 аксиоме Пеано, .

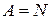Однозначность (?)

Покажем, что 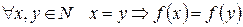. Доказательство проведем методом математической индукции в І форме для натуральных чисел по .

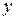База индукции :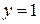

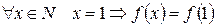, т.е. (?)

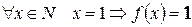Предположим, что 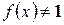. 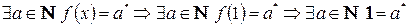, последнее противоречит 1 аксиоме Пеано. Таким образом, предположение неверно.

Индуктивное предположение :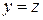

.

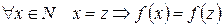Покажем справедливость утверждения для :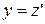

(?)

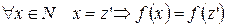Предположим, что .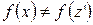

.

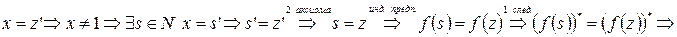
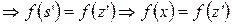Итак, доказано, что 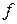является отображением. Остается проверить сюръективность и инъективность 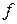. Для чего рассмотрим следующую систему множеств: 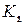, ,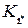…, ,…, 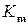где 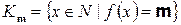. Докажем методом математической индукции в І форме для натуральных чисел по 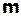, что каждое из этих множеств непустое и одноэлементное, тем самым убедимся в сюръективности и инъективности 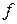, соответственно.

База индукции :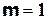

(?)

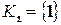Очевидно, что 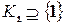, т.к. 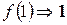. Предположим, что .

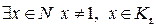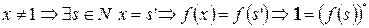. Последнее противоречит 1 аксиоме Пеано, следовательно, предположение неверно.

Индуктивное предположение :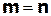

.

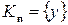Покажем справедливость утверждения для :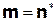

(?)

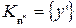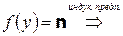
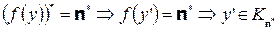. Предположим, что 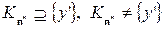. Тогда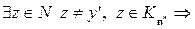 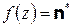. Возможны случаи:

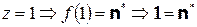§ . Последнее противоречит 1 аксиоме Пеано.

§

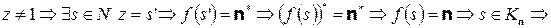
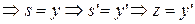, что противоречит условию .

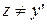Таким образом, в обоих случаях получено противоречие, следовательно, предположение неверно.

что и требовалось доказать.