Упорядоченность полукольца натуральных чисел.
На множестве натуральных чисел определим бинарное отношение  по следующему правилу:
по следующему правилу:
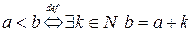
Теорема 3.Отношение  на множестве натуральных чисел является строгим линейным порядком.
на множестве натуральных чисел является строгим линейным порядком.
Доказательство.
Отношение  - порядок на
- порядок на 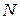 (?)
(?)
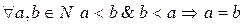 (антисимметричность) (?)
(антисимметричность) (?)
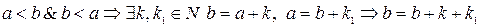 . Возможны случаи:
. Возможны случаи:
§ 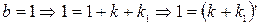 ;
;
§  .
.
В обоих случаях получили противоречие с 1 аксиомой Пеано, следовательно, посылка импликации ложна, а, значит, сама импликация истинна.
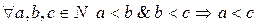 (транзитивность) (?)
(транзитивность) (?)
 .
.
Порядок  - строгий (?)
- строгий (?)
 (антирефлексивность) (?)
(антирефлексивность) (?)
Предположим, что  . Возможны случаи:
. Возможны случаи:
§  ;
;
§  .
.
В обоих случаях получили противоречие с 1 аксиомой Пеано, следовательно, предположение неверно.
Порядок  - линейный (?)
- линейный (?)
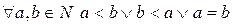 (линейность) (?)
(линейность) (?)
Доказательство проведем методом математической индукции в І форме для натуральных чисел по 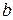 .
.
База индукции 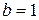 :
:
Возможны случаи:
§ 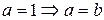 ;
;
§ 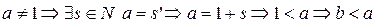 .
.
В обоих случаях дизъюнкция оказалась истинной.
Индуктивное предположение  :
:

Покажем справедливость утверждения для  :
:
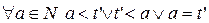 (?)
(?)
Возможны случаи:
§ 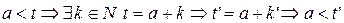 ;
;
§  . Возможны случаи:
. Возможны случаи:
· 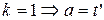 ,
,
· 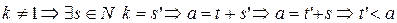 ;
;
§ 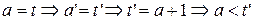 .
.
что и требовалось доказать.
Свойства отношения  :
:
1) 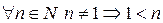 .
.
Дата добавления: 2015-08-21; просмотров: 694;
