Решение. Проверим условие аналитичности функции и найдем ее производную
Проверим условие аналитичности функции  и найдем ее производную. Для этого первоначально найдем действительную и мнимую части функции:
и найдем ее производную. Для этого первоначально найдем действительную и мнимую части функции:
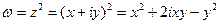
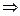
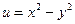 ,
,  .
.
Проверим условия КРЭДа:
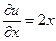 ,
, 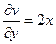
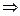
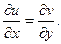
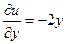 ,
, 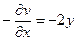
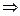
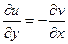 .
.
Условия КРЭДа выполняются по всей плоскости Гаусса, т.е. функция аналитическая Следовательно, существует производная, которую найдем по первой формуле (11):
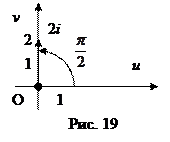
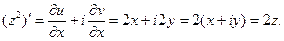
Найдем производную функции в точке 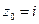 :
:
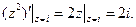
По формуле (16) найдем коэффициент растяжения k: 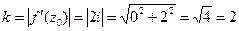 .
.
По формуле (15) найдем угол поворота 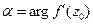 . (В данном случае удобнее изобразить комплексное число 2i (рис. 19)).
. (В данном случае удобнее изобразить комплексное число 2i (рис. 19)). 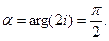
Пример 27.Найти множество точек  , в которых при отображении
, в которых при отображении 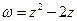 угол поворота
угол поворота 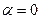 .
.
Дата добавления: 2015-07-14; просмотров: 776;
