Конформные отображения
Пусть в области D на плоскости (z) задана аналитическая функция 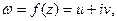 т.е. u(x,y) и v(x,y) – гармоническая пара. Зададим определенное значение
т.е. u(x,y) и v(x,y) – гармоническая пара. Зададим определенное значение 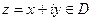 . Этому значению соответствует определенное значение
. Этому значению соответствует определенное значение 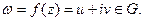 Следовательно, каждой точке z = (x,y) на плоскости (Oxy) соответствует определенная точка ω = (u,v) на плоскости (Оuv) и наоборот, т.е. задается взаимно-однозначное отображение области D плоскости (z) на область G плоскости
Следовательно, каждой точке z = (x,y) на плоскости (Oxy) соответствует определенная точка ω = (u,v) на плоскости (Оuv) и наоборот, т.е. задается взаимно-однозначное отображение области D плоскости (z) на область G плоскости 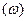 посредством аналитической функции или, что тоже самое, посредством гармонической пары.
посредством аналитической функции или, что тоже самое, посредством гармонической пары.
Определение 34. Если функция аналитическая, то соответствующее отображение называется аналитическим.
Определение 35.Взаимно-однозначное отображение называется регулярным в некоторой замкнутой области D плоскости (Oxy), если
1) функции u(x,y) и v(x,y) – определены, непрерывны и обладают непрерывными частными производными до второго порядка включительно в области D,
2) якобиан 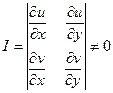 .
.
Дата добавления: 2015-07-14; просмотров: 817;
