Композиция отображений. Обратные отображения.

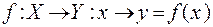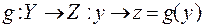Пусть и - два отобра-жения. Тогда отображение

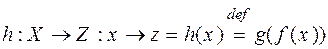
называется композицией (суперпозицией) отображений f и g или сложным отображением; знак « 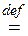» читается как «равняется по определению».

Заметим также, что композиция h отображений f и g обознача-ется символом h = g f. Поэтому по определению

(gf)(x)=g(f(x)).

Термин сложное отображение следует понимать как состав-ное (состоящее из нескольких других) отображение.

Например, отображения – функции 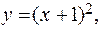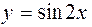, 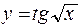- сложные, в том смысле, что каждая состоит из двух функций: первая из функци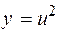й и 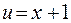; вторая – y = sin v и v = 2x, третья – у = tg t и

Ясно, что имеются композиции функций, состоящие из какого угодно количества входящих в них функций.

Например, функция

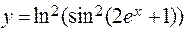
является композицией следующей цепочки из шести функций:

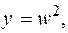w = ln v, v = u², u = sin t, t = 2z+1, .

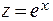Для определения обратного отображения используется всем хорошо известное отображение, так называемое тождественное отображение

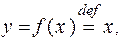
Определённое на множестве X тождественное отображение, обозначается символом .

Если 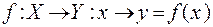- некоторое отображение, то отображение 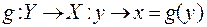называется обратным для f, если выполнены два условия:

1) композиция g· f = id_X или, подробнее, g(f(x))=x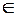, x X,

2) композиция f·g = id_Y или, подробнее, f(g(y))=y,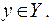

Ясно, что понятие обратного отображения является взаимным: если g – обратное для f отображение, то f – обратное для g.

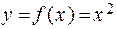
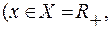
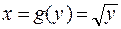
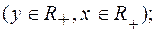
Например, следующие пары отображений – функци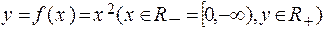й и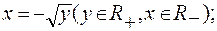

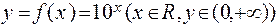и

и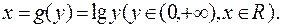

являются парами взаимно обратных функций.

Теорема. Отображение имеет обратное отображение 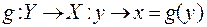тогда и только тогда, когда f – взаимно однозначное (биективное) отображение.

Упражнение. Докажите теорему.