Множества. Общие понятия

МНОЖЕСТВА, ОТОБРАЖЕНИЯ И ФУНКЦИИ

Понятие множества пронизывает все современное естество-знание и, в особенности, математику. Оно приобретает все возра-стающее значение во многих сферах производственной деятельно-сти и – даже – в быту. Это относится также к понятию отображе-ния множеств, частным случаем которого является (числовая) фун-кция. В учебной литературе по высшей математике этим понятиям уделяется недостаточное внимание. Настоящее учебное пособие восполняет пробел. Оно содержит минимальные сведения о множествах и их отображениях. В связи с этим работа может заинтересовать не только студентов но и начинающих преподавателей.

Множества. Общие понятия

Множество – набор, совокупность, собрание каких-либо объ-ектов, называемых его элементами, или точками, обладающих об-щим для них характеристическим свойством. При введении его в рассмотрение постулируется, что понятие множества является пер-вичным и не определяется с помощью иных, если можно так выра-зиться, более первичных и простых понятий. К другим терминам – синонимам понятия множества относятся, например, слова: семей-ство, группа, класс, геометрическое место точек (ГМТ).

При этом множество задаётся либо перечислением его элемен-тов, либо с помощью правила, позволяющего определить принадле-жит или нет данный объект рассматриваемому множеству.

Первый способ годится теоретически для любых конечных мно-жеств, т.е. множеств, состоящих из конечного числа элементов.

В математике (и не только в ней) приходится иметь дело также с множествами бесконечными; например, множеством всех нату-ральных чисел, всех чётных чисел, всех целых чисел, всех прямых на плоскости и т.д.

Если х есть элемент множества А, то пишут: 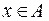или .

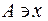Если каждый элемент множества А является в то же время элементом множества В, то А называется частью или подмно-жеством множества В. Записывают это так: 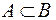или .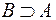

Равенство А=В означает, что 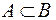и, одновременно .

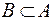Всякое множество А есть подмножество самого себя: 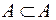(точнее А=А). Пустое множество Ø (т.е. множество не имеющее элементов) также является частью всякого множества А: Ø . Множества А и Ø называют несобственными подмножествами множества А; все остальные подмножества – собственные.

Подмножество множества А, состоящее из всех элементов, удовлетворяющих данному условию S, обозначается через 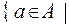а удовлетворяет 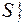. Например, двухэлементное множество .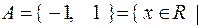

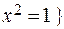Условие S здесь означает, что х удовлетворяет уравнению х² =1; А – есть множество решений этого уравнения.

Объединением двух множеств А и В называется множество элементов, каждый из которых принадлежит хотя бы одному из множеств А и В.

На этом рисунке слева множества А и В

изображены кругами; их объединение -

заштрихованная часть плоскости, покрыва-

А В емая обоими кругами.

Обозначение объединения: .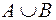

Пересечением (общей частью) множеств А и В называется множество всех тех элементов, каждый из которых содержится в обоих множества А и В. Пересечение обозначается через .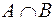

На рисунке слева кругами обозначают-

ся множества А и В; их пересечение

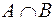- заштрихованная часть плоско-

сти (общая часть кругов А и В).

А В

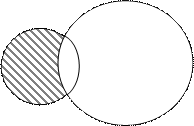Разностью двух множеств А и В (второе не обязательно со-держится в первом) называется множество тех элементов мно- жеств которые не суть элементы множества В.

Разность А и В обозначается через

А \ В. На этом рисунке слева множе-

ства А и изображены кругами; их

разность А\В – заштрихованная

А В часть круга А.

Приведём некоторые свойства операций над множествами.

Коммутативность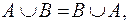

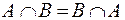
Ассоциативность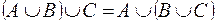

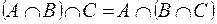
Дистрибутивность пересечения относительно объединения

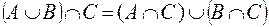
Дистрибутивность объединения относительно пересечения

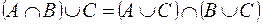
5)

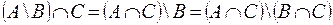
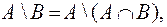
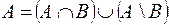
6) Законы двойственности де Моргана

X \ ( 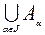) = 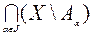, X \ ( ) = ,

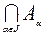J – некоторое множество индексов.