Отображения. Говорят, что задано отображение одного множества Х (≠ Ø) в другое множество Y, если каждому элементу (точке) по неко-торому правилу f поставлен
Говорят, что задано отображение одного множества Х (≠ Ø) в другое множество Y, если каждому элементу (точке) 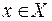 по неко-торому правилу f поставлен в соответствие единственный элемент (точка)
по неко-торому правилу f поставлен в соответствие единственный элемент (точка) 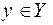 . Иначе говоря, отображение – это тройка (Х, f, Y), в которой Х и Y – множества, а f – указанное выше правило.
. Иначе говоря, отображение – это тройка (Х, f, Y), в которой Х и Y – множества, а f – указанное выше правило.
Для обозначения отображения используются также записи:
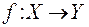 или
или 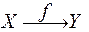
(читается одинаково: отображение «эф» множества «икс» во мно-жество «игрек»), или, подробнее:
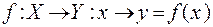
(читается: отображение f множества Х во множество Y, переводя-щее точку 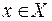 в точку
в точку 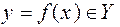 . При этом пишут: y = f(x),
. При этом пишут: y = f(x), 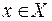 ,
, 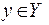 ; точку у называют образом точки х , а х – прообразом точки у (при отображении f); Х называют множеством определения отображения f, а Y – множеством изменения (значений - образов) отображения f.
; точку у называют образом точки х , а х – прообразом точки у (при отображении f); Х называют множеством определения отображения f, а Y – множеством изменения (значений - образов) отображения f.
В случае, когда Y – числовое множество, отображение 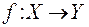 часто называют функцией (на множестве Х).
часто называют функцией (на множестве Х).
Иногда, множество Х называют областью определения, а Y множеством значений функции Это словоупотребление нельзя признать корректным. Во-первых, термин «область» не является вакантным; он употребляется в курсе высшей математики совсем в другом смысле в интегральном исчислении Во-вторых, множество Y правильнее называть именно множеством изменения, а не множеством значений отображения (функции) т.к. множество значений – это образ f(Х) множества Х при отображении 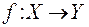 ; в общем случае f(Х) не совпадает с Y.
; в общем случае f(Х) не совпадает с Y.
Приведём некоторые примеры.
1. Х – множество студентов в аудитории, Y – множество стуль-ев в этой же аудитории. Отображение (правило) f заключается в следующем: каждому студенту (точке) 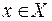 ставится в соответ-ствие тот единственный стул (точка)
ставится в соответ-ствие тот единственный стул (точка) 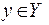 , на котором сидит х. Имеется отображение
, на котором сидит х. Имеется отображение
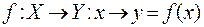 .
. 
2. Х – множество студентов в аудитории. Y=R – множество действительных чисел. Каждое из следующих словосочетаний определяет некоторую функцию: «рост студента», «вес студента», «размер обуви студента» и т.д.
Отображение 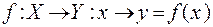 называется:
называется:
1) взаимно однозначным «в» (или инъективным), если образы любых двух различных точек различны;
2) отображением «на» (или сюръективным), если для любого 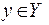 , существует хотя бы один прообраз
, существует хотя бы один прообраз 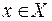 , т.е. такая точка х, образ которой
, т.е. такая точка х, образ которой 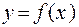 ;
;
3) взаимно однозначным (или биективным), если оно обладает первыми двумя свойствами одновременно.
Эти свойства отображений можно проиллюстрировать с по-мощью только что приведённых примеров. Так отображение при-мера 1 является – по смыслу инъективным (разные студенты сидят на разных стульях); оно будет сюръективным, если нет свободных стульев; в этом случае оно будет и взаимно однозначным (биек-тивным).
В примере 2 отображение «рост студента», например, будет инъективным, если в аудитории нет студентов одинакового роста. В противном случае, оно не является инъективным. Эта же функция «рост студента» не может быть сюрьективной, ибо – в противном случае – в аудитории были бы студенты 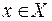 любого наперёд заданного (в том числе, отрицательного) роста
любого наперёд заданного (в том числе, отрицательного) роста 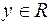 .
.
Дата добавления: 2015-07-24; просмотров: 1260;
