Числовые множества. В процессе изучения математики вводятся уже в средней школе следующие числовые множества.

В процессе изучения математики вводятся уже в средней школе следующие числовые множества.

а) N = {1, 2, 3, … , n, …} - множество натуральных чисел.

б) Z = {0, ±1, ±2, … , ±n, …} - множество целых чисел.

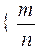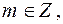
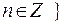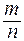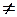в) Q = | - множество рациональных чисел, т.е. множество всевозможных обыкновенных дробей (n 0).

г) R – множество действительных (вещественных) чисел, т.е., грубо говоря, таких чисел, каждое из которых с любой степенью точности может быть приближенно (заменено) рациональным числом. Иначе говоря, R – множество всевозможных десятичных дробей, как конечных, так и бесконечных. При этом всякая обык-новенная дробь 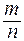(т.е. рациональное число) представляется либо конечной дробью, либо бесконечной периодической дробью. Вся-кая бесконечная непериодическая десятичная дробь называется иррациональным числом.

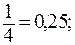
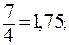
Например, числа 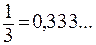(три в периоде) являются рациональными. Число 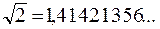является ирра-циональным. Это, правда, требует отдельного доказательства.

Оказывается, что между любыми двумя различными действи-тельными числами всегда имеется бесконечное множество как рациональных, так и иррациональных чисел.

д) [а, b], [а, b), (а, b], (а, b), [а, +∞), (-∞, b], (а, +∞), (-∞, b) – интервалы (отрезки, промежутки) числовой прямой (т.е. множества действительных чисел) R, которые состоят из чисел 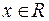, удовлетворяющих, соответственно, неравенствам: а ≤ х ≤ b, а ≤ х <b, а < х ≤ b, а < х < b, а ≤ х < +∞, -∞ < х ≤ b, а < х < +∞, -∞ < х < b. В этих обозначениях обычно предполагается, что а < b.

е) Для любой точки (числа) 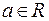и любого числа 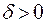определено множество – интервал (а – δ, а + δ), симметричный относительно точки а. Этот интервал называется δ-окрестностью точки а, а δ – её радиусом. Эта окрестность определяется неравенствами:

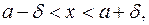или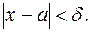

Т.о. точка 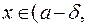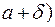тогда и только тогда, когда х удовлетворяет указанным неравенствам.