Свойства регулярных отображений
1. Регулярное отображение непрерывно в обе стороны, т.е. достаточно близким точкам при отображении в одну сторону и в другую соответствуют сколь угодно близкие точки.
2. При регулярном отображении внутренние точки области D переходят во внутренние точки области G; граничные точки области D – в граничные точки области G и, наоборот, при обратном отображении.
3. При регулярном отображении кривая отображается в кривую.
4. Абсолютная величина якобиана при регулярном отображении равна пределу отношения меры отображенной области и первоначальной при стягивании их в точку:
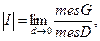 d – диаметр области.
d – диаметр области.
Таким образом,  – коэффициент растяжения областей или величина искажения масштаба в точке z при отображении с помощью функции
– коэффициент растяжения областей или величина искажения масштаба в точке z при отображении с помощью функции 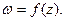
Выведем формулу для нахождения коэффициента:
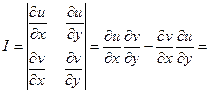 (по КРЭДу)
(по КРЭДу) 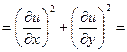 или
или 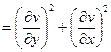 .
.
Тогда, коэффициент растяжения будет равен 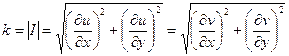 . (14)
. (14)
Определение 36.Регулярное отображение области D плоскости (Oxy) на область G плоскости (Оuv) посредством гармонической пары или, что то же самое, аналитической функции, называется конформным, если в каждой точке оно обладает свойствами сохранения углов и постоянства растяжений.
Если представить себе плоскости (z) и  совмещенными, то каждый малый вектор
совмещенными, то каждый малый вектор  с вершиной в точке z0 при отображении будет перенесен вершиной в
с вершиной в точке z0 при отображении будет перенесен вершиной в 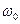 , растянут в k0 раз и повернут на угол α0. Поэтому и вся малая окрестность точки z0 при рассматриваемом отображении испытает поступательный перенос, всестороннее растяжение и поворот. Образ каждой малой фигуры, расположенной в области G, будет, с точностью до малых высшего порядка, геометрически подобен прообразу, т.е. малый круг переходит в круг, а углы между пересекающимися линиями сохраняются.
, растянут в k0 раз и повернут на угол α0. Поэтому и вся малая окрестность точки z0 при рассматриваемом отображении испытает поступательный перенос, всестороннее растяжение и поворот. Образ каждой малой фигуры, расположенной в области G, будет, с точностью до малых высшего порядка, геометрически подобен прообразу, т.е. малый круг переходит в круг, а углы между пересекающимися линиями сохраняются.
Лемма. При аналитическом отображении ориентация плоскости сохраняется, т.е. если обходить малый замкнутый контур плоскости (z) в некотором направлении, то и образ будет обходиться в том же направлении. И обратно, если некоторое отображение плоскости сохраняет подобие бесконечно малых фигур (или даже только углы между пересекающимися линиями) и ориентацию плоскости, то это отображение аналитическое.
В связи со сказанным можно дать другое определение конформности:
Определение 37.Взаимно однозначное отображение некоторой плоской области, при котором сохраняются подобие бесконечно малых фигур и ориентация плоскости, называется конформным; если подобие сохраняется, но ориентация меняется на противоположную, то отображение называется антиконформным.
Теорема 8.Отображение посредством аналитической функции конформно при условии, что якобиан 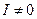 .
.
Рассмотрим подробнее сказанное о сохранении углов и постоянстве растяжений при конформных отображениях.
Пусть 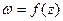 – аналитическая функция в области D. Пусть задается взаимно-однозначное отображение области D плоскости (z) на область G плоскости
– аналитическая функция в области D. Пусть задается взаимно-однозначное отображение области D плоскости (z) на область G плоскости 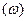 посредством данной аналитической функции. Если точка (x,y) на плоскости (Oxy) описывает некоторую линию Г, расположенную в области D, то соответствующая точка (u,v) на плоскости (Оuv) опишет линию Г /, расположенную в области G (рис. 15).
посредством данной аналитической функции. Если точка (x,y) на плоскости (Oxy) описывает некоторую линию Г, расположенную в области D, то соответствующая точка (u,v) на плоскости (Оuv) опишет линию Г /, расположенную в области G (рис. 15).
Линию Г / называют отображением или образом линии Г на плоскость (Оuv) с помощью аналитической функции.
1) О сохранении углов.
Возьмем на линии Г точку 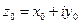 (см. рис. 15). Этой точке на линии Г / соответствует точка
(см. рис. 15). Этой точке на линии Г / соответствует точка 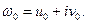 Проведем к линии Г касательную L в точке (x0, y0), а к линии Г / – касательную
Проведем к линии Г касательную L в точке (x0, y0), а к линии Г / – касательную 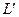 в точке
в точке 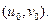
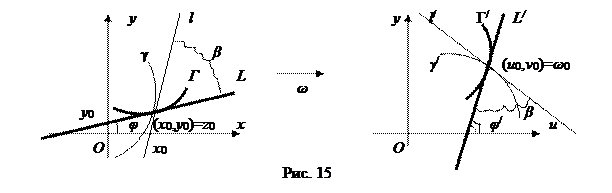
Пусть α – угол, на который нужно повернуть касательную L, чтобы ее направление совпало с направлением прямой  , т.е. это угол между касательными к первоначальной и отображенной кривым:
, т.е. это угол между касательными к первоначальной и отображенной кривым: 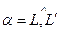 .
.
Можно доказать, что 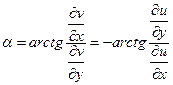 .
.
Пусть 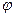 – угол между осью (Ох) и касательной L к кривой Г, тогда
– угол между осью (Ох) и касательной L к кривой Г, тогда 
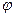 /– угол между осью (Оu) и касательной
/– угол между осью (Оu) и касательной 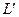 к кривой Г/,
к кривой Г/, 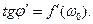
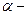 угол между L и
угол между L и 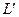 . Если
. Если 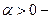 поворот от L к
поворот от L к 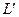 происходит против часовой стрелки, если
происходит против часовой стрелки, если 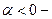 поворот от L к
поворот от L к 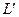 происходит по часовой стрелке.
происходит по часовой стрелке.
Геометрический смысл аргумента производной:
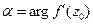 – (15)
– (15)
аргумент производной функции 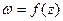 в точке
в точке 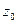 геометрически равен углу
геометрически равен углу 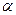 , на который нужно повернуть касательную L в точке
, на который нужно повернуть касательную L в точке 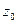 к кривой Г, чтобы получить касательную
к кривой Г, чтобы получить касательную 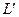 в точке ω0 к образу этой кривой Г/.
в точке ω0 к образу этой кривой Г/.
Рассмотрим другую линию γ, также проходящую через точку (x0, y0), и ее отображение – линию 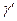 , проходящую через точку
, проходящую через точку 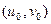 (рис. 15). Пусть l – касательная к кривой γ в точке (x0, y0),
(рис. 15). Пусть l – касательная к кривой γ в точке (x0, y0), 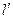 – касательная к кривой
– касательная к кривой 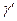 в точке
в точке 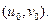
Для того чтобы направление прямой l совпало с направлением прямой 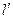 надо и в этом случае прямую l повернуть на угол α, т.к. α зависит только от значения производной и не зависит от уравнения кривой.
надо и в этом случае прямую l повернуть на угол α, т.к. α зависит только от значения производной и не зависит от уравнения кривой.
Вывод 1. Две произвольные линии, пересекающиеся в точке (x0, y0), отображаются посредством функции 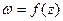 в две соответствующие линии, пересекающиеся в точке
в две соответствующие линии, пересекающиеся в точке 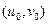 так, что угол β между касательными к данным и между касательными к отображенным линиям один и тот же.
так, что угол β между касательными к данным и между касательными к отображенным линиям один и тот же.
Замечание. Из свойства сохранения углов вытекает, в частности, что линии 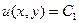 и
и 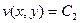 плоскости (x,y) образуют два взаимно ортогональных семейства линий. Это дает возможность, задаваясь различными аналитическими функциями
плоскости (x,y) образуют два взаимно ортогональных семейства линий. Это дает возможность, задаваясь различными аналитическими функциями 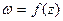 , получать разнообразные ортогональные системы координат на плоскости.
, получать разнообразные ортогональные системы координат на плоскости.
2) О постоянстве растяжений.
Рассмотрим коэффициент растяжения k. Пусть аналитическая функция 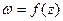 отображает кривую Г1 в кривую γ1, кривую Г2 в кривую γ2, причем точка
отображает кривую Г1 в кривую γ1, кривую Г2 в кривую γ2, причем точка 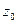 отображается в точку ω0,
отображается в точку ω0, 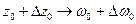 ,
, 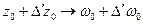 (рис. 16).
(рис. 16).
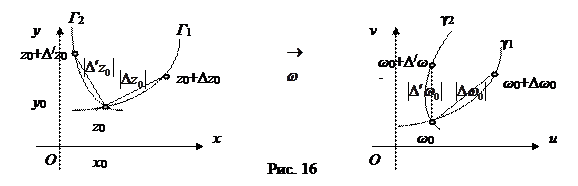
Тогда 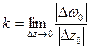 – предел отношения растяжений или
– предел отношения растяжений или 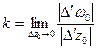 .
.
Замечание. При конформном отображении сохраняется подобие лишь бесконечно малых фигур, тогда как форма конечных фигур может существенно измениться. Например, квадрат плоскости (z), разбитый на 4 квадратика, может отобразиться на криволинейную фигуру с прямыми углами на плоскости  (рис. 17). Дело в том, что хотя каждый малый участок плоскости (z) при отображении испытывает всестороннее растяжение и поворот, но для разных участков коэффициенты растяжения и углы поворота различны, что и приводит к такому искажению.
(рис. 17). Дело в том, что хотя каждый малый участок плоскости (z) при отображении испытывает всестороннее растяжение и поворот, но для разных участков коэффициенты растяжения и углы поворота различны, что и приводит к такому искажению.

Пусть отрезок АВ посредством аналитической функции 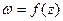 отображается в кривую
отображается в кривую 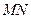 (рис. 18). Тогда коэффициент растяжения
(рис. 18). Тогда коэффициент растяжения 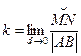 – предел отношения длины дуги к длине отрезка. Следовательно, и любой другой отрезок растягивается ровно в k раз в плоскости (Оuv) при этом отображении.
– предел отношения длины дуги к длине отрезка. Следовательно, и любой другой отрезок растягивается ровно в k раз в плоскости (Оuv) при этом отображении.

При k > 1 имеет место растяжение, при k < 1 – сжатие.
Ранее вывели, что коэффициент растяжения может быть найден по формуле (14): 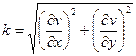 .
.
Из теоремы 5 известно, что производная аналитической функции 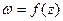 в точке z0 находится по формуле (11):
в точке z0 находится по формуле (11): 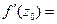
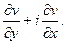 Найдем модуль полученной после дифференцирования ФКП :
Найдем модуль полученной после дифференцирования ФКП : 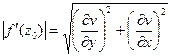 и сравним полученное выражение с выражением (14). Видно, что
и сравним полученное выражение с выражением (14). Видно, что 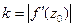 . Для существования отображения должно быть
. Для существования отображения должно быть 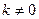 , что гарантирует теорема 8, так как
, что гарантирует теорема 8, так как 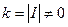 .
.
Геометрический смысл модуля производной:
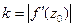 – (16)
– (16)
модуль производной функции 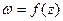 в точке
в точке 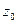 геометрически равен коэффициенту растяжения в точке
геометрически равен коэффициенту растяжения в точке 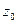 при отображении
при отображении 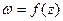 .
.
Вывод 2. При отображении аналитической функцией наблюдается постоянство растяжений (сжатий), следовательно, отображение, осуществляемое аналитической функцией, конформно.
Определение 38.Функция 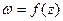 называется однолистной в области D, если любым различным значениям
называется однолистной в области D, если любым различным значениям 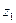
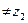 , взятым из области D, соответствуют различные значения функции
, взятым из области D, соответствуют различные значения функции 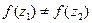 . Другими словами, если функция, обратная к
. Другими словами, если функция, обратная к 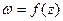 , однозначная, то отображение называется однолистным.
, однозначная, то отображение называется однолистным.
Однолистность означает, что при отображении 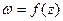 плоскость (z) покрывает плоскость
плоскость (z) покрывает плоскость 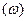 только один раз.
только один раз.
Критерий конформности отображения:Для того чтобы отображение области D, задаваемое функцией 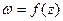 , было конформным, необходимо и достаточно, чтобы
, было конформным, необходимо и достаточно, чтобы 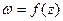 была однолистной и аналитической в области D функцией, причем
была однолистной и аналитической в области D функцией, причем 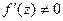 всюду в D.
всюду в D.
Общий вывод из 1) и 2).Геометрический смысл модуля и аргумента производной аналитической функции состоит в том, что при отображении, осуществляемом этой функцией, удовлетворяющей условию 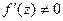 , коэффициент растяжения k определяет коэффициент преобразования подобия бесконечно малого линейного элемента в точке z0 , а α – угол поворота этого элемента.
, коэффициент растяжения k определяет коэффициент преобразования подобия бесконечно малого линейного элемента в точке z0 , а α – угол поворота этого элемента.
Пример 26.Найти коэффициент растяжения и угол поворота в точке 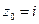 для отображения
для отображения 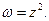
Дата добавления: 2015-07-14; просмотров: 1402;
