Дифференциальное уравнение гармонических колебаний.
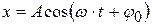 , (4.1)
, (4.1)
Скорость 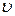 колеблющейся материальной точки получим, продифференцировав (4.1) по времени:
колеблющейся материальной точки получим, продифференцировав (4.1) по времени:
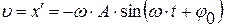 . (4.5)
. (4.5)
Продифференцировав (4.5), получим ускорение а:
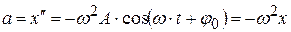 . (4.6)
. (4.6)
Или:
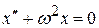 . (4.7)
. (4.7)
Выражение (4.7) описывает гармонические колебания величины x и называется дифференциальным уравнением гармонического осциллятора. Его решением является гармоническая функция (4.1). Если вторая производная по времени какой-либо физической величины (не обязательно смещения) пропорциональна самой величине с противоположным знаком, то данная физическая величина изменяется со временем по гармоническому закону.
3. Пружинный, физический и математический маятники
По второму закону Ньютона найдём из (4.6) силу, действующую на колеблющееся тело:
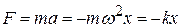 , (4.8)
, (4.8)
где принято обозначение
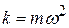 . (4.9)
. (4.9)
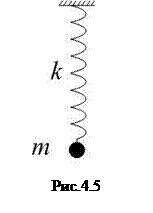 Сила пропорциональна смещению из положения равновесия и противоположна ему; её называют возвращающей (направлена к положению равновесия), или квазиупругой (описывается формально так же, как и упругая сила по закону Гука). Для пружинного маятника (рис.4.5) коэффициент пропорциональности
Сила пропорциональна смещению из положения равновесия и противоположна ему; её называют возвращающей (направлена к положению равновесия), или квазиупругой (описывается формально так же, как и упругая сила по закону Гука). Для пружинного маятника (рис.4.5) коэффициент пропорциональности 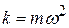 имеет смысл жёсткости пружины. Круговая частота и период колебаний такого маятника:
имеет смысл жёсткости пружины. Круговая частота и период колебаний такого маятника:
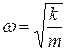 ; (4.10)
; (4.10)
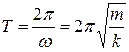 . (4.11)
. (4.11)
Физическим маятником называется твёрдое тело, способное колебаться в поле силы тяжести относительно оси, не проходящей через центр масс (рис.4.6).
Длина физического маятника  – это расстояние между центром масс С и осью вращения (точка О). Плечо силы тяжести равно
– это расстояние между центром масс С и осью вращения (точка О). Плечо силы тяжести равно
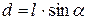 , (4.12)
, (4.12)
где 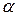 – угол отклонения из положения равновесия. Момент силы тяжести относительно оси вращения
– угол отклонения из положения равновесия. Момент силы тяжести относительно оси вращения
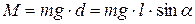 ; (4.13)
; (4.13)
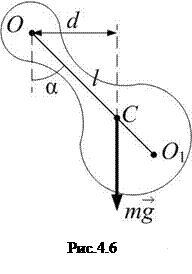 для малых углов отклонения
для малых углов отклонения
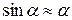 ,
,
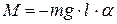 . (4.14)
. (4.14)
Знак «–» в (4.14) поставили потому, что проекция углового перемещения на ось вращения противоположна по знаку проекции момента силы. По закону динамики для вращательного движения (3.13) 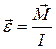 , где
, где 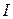 – момент инерции маятника относительно оси вращения тогда угловое ускорение
– момент инерции маятника относительно оси вращения тогда угловое ускорение
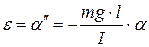 ,
,
или
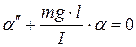 . (4.15)
. (4.15)
Уравнение (4.15) – это дифференциальное уравнение гармонических колебаний типа (4.7), где роль переменной величины играет угол отклонения маятника:
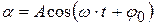 ,
,
а коэффициент при 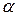 – квадрат круговой частоты:
– квадрат круговой частоты:
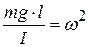 .
.
Период колебаний физического маятника
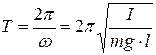 . (4.16)
. (4.16)
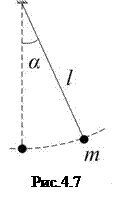 Частным случаем физического маятника является маятник математический: материальная точка (тело, размерами которого можно пренебречь), подвешенная на нерастяжимой невесомой нити (рис.4.7). Для материальной точки момент инерции
Частным случаем физического маятника является маятник математический: материальная точка (тело, размерами которого можно пренебречь), подвешенная на нерастяжимой невесомой нити (рис.4.7). Для материальной точки момент инерции 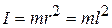 ; тогда
; тогда
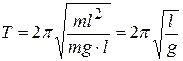 . (4.17)
. (4.17)
Введём определение для физического маятника: приведённая длина физического маятника – это длина такого математического маятника, который имеет тот же период колебаний. По определению
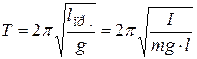 ,
,
откуда
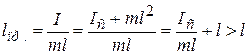 .
.
Здесь 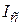 – момент инерции тела относительно оси, проходящей через центр масс;
– момент инерции тела относительно оси, проходящей через центр масс; 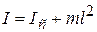 – по теореме Штейнера. Приведённая длина физического маятника
– по теореме Штейнера. Приведённая длина физического маятника 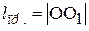 (рис.4.6) всегда больше его длины
(рис.4.6) всегда больше его длины 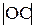 ; в частном случае математического маятника они совпадают. Точка
; в частном случае математического маятника они совпадают. Точка 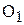 называется точкой качаний; она с точкой подвеса О обладает свойством взаимности: если маятник перевернуть и подвесить за
называется точкой качаний; она с точкой подвеса О обладает свойством взаимности: если маятник перевернуть и подвесить за 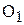 , период колебаний будет таким же.
, период колебаний будет таким же.
Дата добавления: 2015-04-10; просмотров: 1764;
