Колебания и волны
Предисловие
Обращаю внимание студентов на то, что ЭТОТ материал в школе не рассматривался АБСОЛЮТНО (кроме понятия момента силы).
План
1. Закон динамики вращательного движения
a. Закон динамики вращательного движения
b. Момент силы
c. Момент пары сил
d. Момент инерции
2. Моменты инерции некоторых тел:
a. Кольцо (тонкостенный цилиндр)
b. Толстостенный цилиндр
c. Сплошной цилиндр
d. Шар
e. Тонкий стержень
3. Теорема Штейнера
4. Момент импульса тела. Изменение момента импульса тела. Импульс момента силы. Закон сохранения момента импульса
5. Работа при вращательном движении
6. Кинетическая энергия вращения
7.  Сопоставление величин и законов для поступательного и вращательного движения
Сопоставление величин и законов для поступательного и вращательного движения
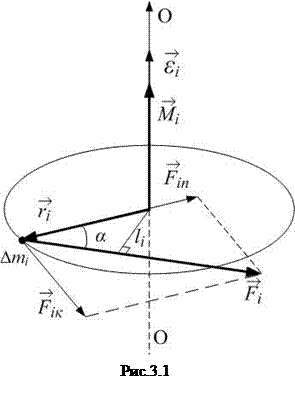
1a.  Рассмотрим твердое тело, которое может вращаться вокруг неподвижной оси ОО (рис.3.1). Разобьем это твердое тело на отдельные элементарные массы Δmi. Равнодействующую всех сил, приложенных к Δmi, обозначим через
Рассмотрим твердое тело, которое может вращаться вокруг неподвижной оси ОО (рис.3.1). Разобьем это твердое тело на отдельные элементарные массы Δmi. Равнодействующую всех сил, приложенных к Δmi, обозначим через 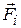 . Достаточно рассмотреть случай, когда сила
. Достаточно рассмотреть случай, когда сила 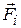 лежит в плоскости, перпендикулярной оси вращения: составляющие сил, параллельные оси, не могут влиять на вращение тела, так как ось закреплена. Тогда уравнение второго закона Ньютона для касательных составляющих силы и ускорения запишется в виде:
лежит в плоскости, перпендикулярной оси вращения: составляющие сил, параллельные оси, не могут влиять на вращение тела, так как ось закреплена. Тогда уравнение второго закона Ньютона для касательных составляющих силы и ускорения запишется в виде:
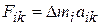 . (3.1)
. (3.1)
Нормальная составляющая силы  обеспечивает центростремительное ускорение и на угловое ускорение не влияет. Из (1.27):
обеспечивает центростремительное ускорение и на угловое ускорение не влияет. Из (1.27): 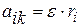 ,где
,где 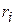 – радиус вращения i-той точки. Тогда
– радиус вращения i-той точки. Тогда
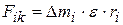 . (3.2)
. (3.2)
Умножим обе части (3.2) на 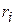 :
:
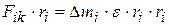 . (3.3)
. (3.3)
Заметим, что
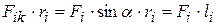 , (3.4)
, (3.4)
где α – угол между вектором силы 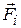 и радиус-вектором точки
и радиус-вектором точки  (рис.3.1),
(рис.3.1), 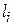 – перпендикуляр, опущенный на линию действия силы из центра вращения (плечо силы).
– перпендикуляр, опущенный на линию действия силы из центра вращения (плечо силы).  Введём понятие момента силы
Введём понятие момента силы 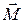 .
.
1b. Моментом силы относительно оси называется вектор, направленный по оси вращения и связанный с направлением силы правилом буравчика, модуль которого равен произведению силы на ее плечо: 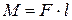 . Плечо силы l относительно оси вращения – это кратчайшее расстояние от линии действия силы до оси вращения. Размерность момента силы:
. Плечо силы l относительно оси вращения – это кратчайшее расстояние от линии действия силы до оси вращения. Размерность момента силы:
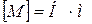 .
.
В векторной форме момент силы относительно точки:
 . (3.5)
. (3.5)
Вектор момента силы перпендикулярен и силе, и радиус-вектору точки её приложения:
 ;
; 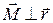 .
.
 Если вектор силы перпендикулярен оси, то вектор момента силы направлен по оси по правилу правого винта, а величина момента
Если вектор силы перпендикулярен оси, то вектор момента силы направлен по оси по правилу правого винта, а величина момента 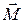 силы относительно этой оси (проекция на ось) определяется формулой (3.4):
силы относительно этой оси (проекция на ось) определяется формулой (3.4):
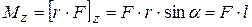 . (3.6)
. (3.6)
Момент силы зависит и от величины силы, и от плеча силы. Если сила параллельна оси, то 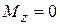 .
.
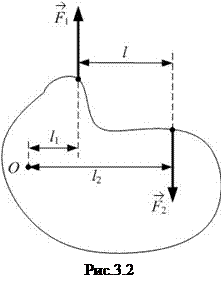
1c. Пара сил – это две равные по величине и противоположные по направлению силы, линии действия которых не совпадают (рис.3.2). Плечо пары сил – это расстояние между линиями действия сил. Найдём суммарный момент пары сил 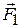 и
и 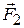 (
( 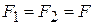 ) в проекции на ось, проходящую через точку О:
) в проекции на ось, проходящую через точку О:
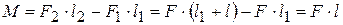 .
.
То есть момент пары сил равен произведению величины силы на плкчо пары:
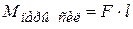 . (3.6)
. (3.6)
Вернёмся к (3.3). С учётом (3.4) и (3.6):
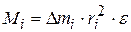 . (3.7)
. (3.7)
1d. Определение: скалярная величина 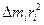 , равная произведению массы материальной точки на квадрат ее расстояния до оси, называется моментом инерции материальной точки относительно оси ОО:
, равная произведению массы материальной точки на квадрат ее расстояния до оси, называется моментом инерции материальной точки относительно оси ОО:
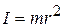 . (3.8)
. (3.8)
Размерность момента инерции
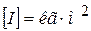 .
.
Из (3.7):
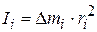 ;
;
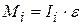 . (3.9)
. (3.9)
Векторы 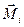 и
и 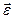 совпадают по направлению с осью вращения, связаны с направлением вращения по правилу буравчика, поэтому равенство (3.9) можно переписать в векторной форме:
совпадают по направлению с осью вращения, связаны с направлением вращения по правилу буравчика, поэтому равенство (3.9) можно переписать в векторной форме:
 ;
;
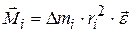 . (3.10)
. (3.10)
Просуммируем (3.10) по всем элементарным массам, на которые разбито тело:
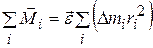 . (3.11)
. (3.11)
Здесь учтено, что угловое ускорение всех точек твердого тела одинаково, и его можно вынести за знак суммы. В левой части равенства стоит сумма моментов всех сил (и внешних, и внутренних), приложенных к каждой точке тела. Но по третьему закону Ньютона, силы, с которыми точки тела взаимодействуют друг с другом (внутренние силы), равны по величине и противоположны по направлению и лежат на одной прямой, поэтому их моменты компенсируют друг друга. Таким образом, в левой части (3.11) остается суммарный момент только внешних сил: 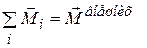 .
.
Сумма произведений элементарных масс на квадрат их расстояний от оси вращения называется моментом инерции твердого тела относительно данной оси:
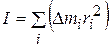 . (3.12)
. (3.12)
Таким образом, 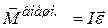 ; – это и есть основной закон динамики вращательного движения твёрдого тела (аналог второго закона Ньютона
; – это и есть основной закон динамики вращательного движения твёрдого тела (аналог второго закона Ньютона 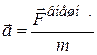 ): угловое ускорение тела прямо пропорционально суммарному моменту внешних сил и обратно пропорционально моменту инерции тела:
): угловое ускорение тела прямо пропорционально суммарному моменту внешних сил и обратно пропорционально моменту инерции тела:
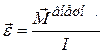 . (3.13)
. (3.13)
Момент инерции Iтвердого тела является мерой инертных свойств твердого тела при вращательном движении и аналогичен массе тела во втором законе Ньютона. Он существенно зависит не только от массы тела, но и от ее распределения относительно оси вращения (в направлении, перпендикулярном оси).
В случае непрерывного распределения массы сумма в (3.12) сводится к интегралу по всему объему тела:
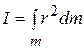 . (3.14)
. (3.14)
2a. Момент инерции тонкого кольца относительно оси, проходящей через его центр перпендикулярно плоскости кольца.
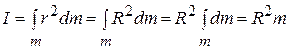 ,
,
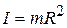 , (3.15)
, (3.15)
поскольку для любого элемента кольца 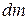 его расстояние до оси одинаково и равно радиусу кольца:
его расстояние до оси одинаково и равно радиусу кольца:  .
.
2b. Толстостенный цилиндр (диск) с внутренним радиусом 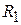 и внешним радиусом
и внешним радиусом 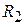 .
.
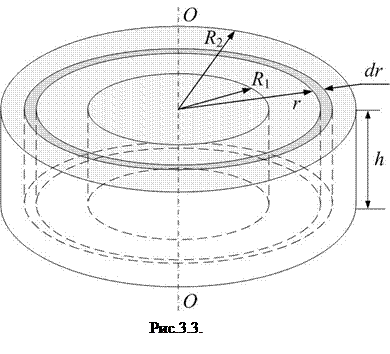
Вычислим момент инерции однородного диска плотностью ρ, высотой h, внутренним радиусом 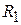 и внешним радиусом
и внешним радиусом 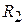 (рис.3.3) относительно оси, проходящей через центр масс перпендикулярно плоскости диска. Разобьем диск на тонкие кольца толщиной
(рис.3.3) относительно оси, проходящей через центр масс перпендикулярно плоскости диска. Разобьем диск на тонкие кольца толщиной 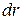 и высотой
и высотой 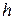 так, что внутренний радиус кольца равен
так, что внутренний радиус кольца равен 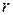 , внешний –
, внешний –  . Объем такого кольца
. Объем такого кольца 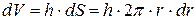 , где
, где  – площадь основания тонкого кольца. Его масса:
– площадь основания тонкого кольца. Его масса:
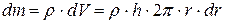 . (3.16)
. (3.16)
Подставим 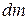 в (3.14) и проинтегрируем по r (
в (3.14) и проинтегрируем по r ( 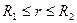 ):
):
 |
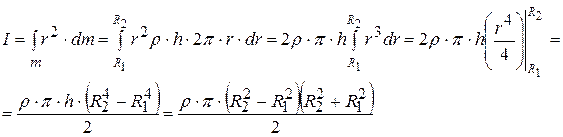
Масса диска 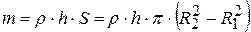 , тогда окончательно:
, тогда окончательно:
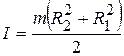 . (3.17)
. (3.17)
2c. Сплошной цилиндр (диск).
В частном случае сплошного диска или цилиндра радиусом R подставим в (3.17) R1=0, R2=R и получим:
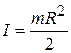 . (3.18)
. (3.18)
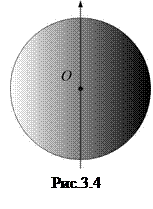
2d. Шар.
Момент инерции шара радиуса R и массой 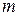 относительно оси, проходящей через его центр (рис.3.4), равен (без доказательства):
относительно оси, проходящей через его центр (рис.3.4), равен (без доказательства):
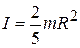 . (3.19)
. (3.19)
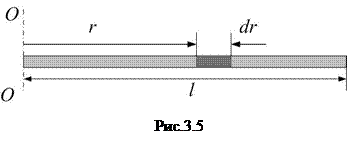
2e. Момент инерции тонкого стержня массой 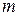 и длиной
и длиной  относительно оси, проходящей через его конец перпендикулярно стержню (рис.3.5).
относительно оси, проходящей через его конец перпендикулярно стержню (рис.3.5).
Стержень разобьём на бесконечно малые участки длиной 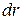 . Масса такого участка
. Масса такого участка 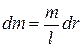 . Подставим в (3.14) и проинтегрируем от 0 до
. Подставим в (3.14) и проинтегрируем от 0 до  :
:
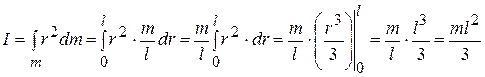 ,
,
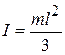 . (3.20)
. (3.20)
Если ось проходит через центр стержня перпендикулярно ему, можно рассчитать момент инерции половины стержня по (3.20) и затем удвоить:
 . (3.21)
. (3.21)
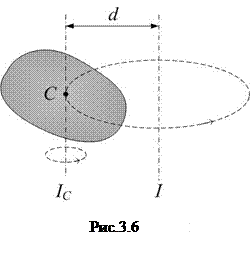 3. Если ось вращения не проходит через центр масс тела (рис.3.6), вычисления по формуле (3.14) могут быть довольно сложными. В этом случае расчет момента инерции облегчается применением теоремы Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции Ic тела относительно оси, проходящей через центр масс тела параллельно данной оси, и произведения массы тела на квадрат расстояния
3. Если ось вращения не проходит через центр масс тела (рис.3.6), вычисления по формуле (3.14) могут быть довольно сложными. В этом случае расчет момента инерции облегчается применением теоремы Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции Ic тела относительно оси, проходящей через центр масс тела параллельно данной оси, и произведения массы тела на квадрат расстояния 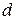 между осями :
между осями :
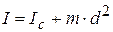 . (3.22)
. (3.22)
Посмотрим, как работает теорема Штейнера, если применить её к стержню:
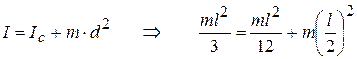 .
.
Нетрудно убедиться, что получилось тождество, поскольку в этом случае расстояние между осями равно половине длины стержня 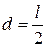 .
.
4. Момент импульса тела. Изменение момента импульса тела. Импульс момента силы. Закон сохранения момента импульса.
Из закона динамики вращательного движения 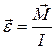 и определения углового ускорения
и определения углового ускорения  следует:
следует:
 .
.
Если 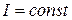 , то
, то 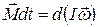 . Введём момент импульса
. Введём момент импульса  твёрдого тела как
твёрдого тела как
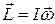 ; (3.23)
; (3.23)
тогда
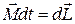 . (3.24)
. (3.24)
Соотношение (3.24) – это основной закон динамики твёрдого тела для вращательного движения. Его можно переписать так:
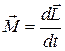 , (3.24)
, (3.24)
и тогда это будет аналог второго закона Ньютона для поступательного движения в импульсной форме (2.5)
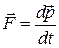 . (2.5)
. (2.5)
Выражение (3.24) можно проинтегрировать:
 (3.25)
(3.25)
и сформулировать закон изменения момента импульса: изменение момента импульса тела равно импульсу суммарного момента внешних сил. Величина 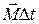 называется импульсом момента силы и аналогична импульсу силы
называется импульсом момента силы и аналогична импульсу силы 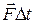 в формулировке второго закона Ньютона для поступательного движения (2.2)
в формулировке второго закона Ньютона для поступательного движения (2.2) 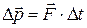 ; момент импульса
; момент импульса 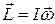 является аналогом импульса
является аналогом импульса 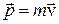 .
.
Размерность момента импульса
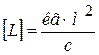 .
.
Момент импульса твёрдого тела относительно его оси вращения – это вектор, направленный по оси вращения по правилу буравчика.
Момент импульса материальной точки относительно точки О (рис.3.6) – это:
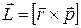 , (3.26)
, (3.26)
где 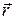 – радиус-вектор материальной точки,
– радиус-вектор материальной точки, 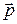 – её импульс. Вектор момента импульса
– её импульс. Вектор момента импульса  направлен по правилу буравчика перпендикулярно плоскости, в которой лежат векторы
направлен по правилу буравчика перпендикулярно плоскости, в которой лежат векторы 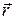 и
и 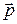 : на рис.3.7 – к нам из-за рисунка. Величина момента импульса
: на рис.3.7 – к нам из-за рисунка. Величина момента импульса
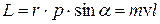 .
.
Твёрдое тело, вращающееся относительно оси, разобьём на элементарные массы 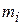 и просуммируем по всему телу моменты импульса каждой массы (то же самое можно записать в виде интеграла; это непринципиально):
и просуммируем по всему телу моменты импульса каждой массы (то же самое можно записать в виде интеграла; это непринципиально):
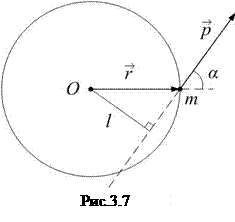
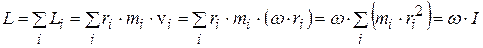 .
.
Поскольку угловая скорость всех точек одинакова и направлена по оси вращения, то можно записать в векторной форме:
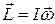 . (3.23)
. (3.23)
Таким образом, доказана эквивалентность определений (3.23) и (3.26).
Если суммарный момент внешних сил равен нулю, то момент импульса системы не изменяется (см.3.25):
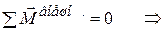
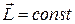 . Это закон сохранения момента импульса. Это возможно, когда:
. Это закон сохранения момента импульса. Это возможно, когда:
а) система замкнута (или 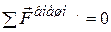 );
);
б) у внешних сил нет касательных составляющих (вектор силы проходит через ось/центр вращения);
в) внешние силы параллельны закреплённой оси вращения.
Примеры использования/действия закона сохранения момента импульса:
1. гироскоп;
2. скамья Жуковского;
3. фигуристка на льду.
5. Работа при вращательном движении.
Пусть тело повернулось на угол  под действием силы
под действием силы 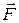 и угол между перемещением
и угол между перемещением 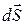 и силой равен
и силой равен 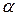 ;
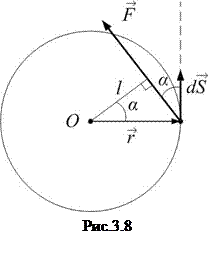
; 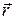 – радиус-вектор точки приложения силы (рис.3.8), тогда работа силы равна:
– радиус-вектор точки приложения силы (рис.3.8), тогда работа силы равна:
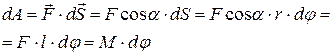
поскольку 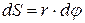 (1.22) и
(1.22) и 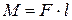 (3.6).
(3.6).
Итак,
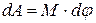 , (3.24)
, (3.24)
или
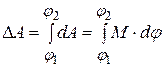 . (3.25)
. (3.25)
6. Кинетическая энергия вращения.
Пусть тело вращается относительно закреплённой оси с угловой скоростью 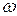 . Разобьём его мысленно на элементарные массы
. Разобьём его мысленно на элементарные массы 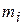 и просуммируем кинетические энергии:
и просуммируем кинетические энергии:
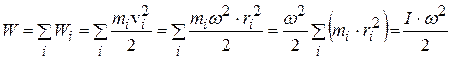 .
.
Здесь воспользовались формулой связи угловой и линейной скорости 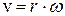 (1.23) и определением момента инерции твёрдого тела
(1.23) и определением момента инерции твёрдого тела 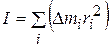 (3.12). Итак, кинетическая энергия вращающегося тела равна:
(3.12). Итак, кинетическая энергия вращающегося тела равна:
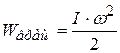 . (3.26)
. (3.26)
Если тело одновременно ещё и движется поступательно (например, тело катится), то полная кинетическая энергия его равна:
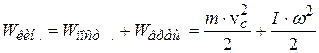 ,
,
где  – скорость поступательного движения центра масс.
– скорость поступательного движения центра масс.
7. Сопоставление величин и законов для поступательного и вращательного движения.
Аналогия между поступательным и вращательным движениями (см. лекцию 1) продолжена в табл.2.1:
Таблица 2.1
| Величина/закон | Поступательное движение | Вращательное движение |
| Перемещение | 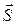
| 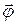
|
| Скорость | 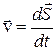
| 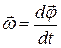
|
| Ускорение | 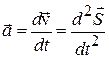
| 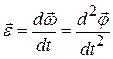
|
| Сила; момент силы | 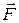
| 
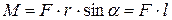
|
| Масса; момент инерции | 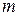
| 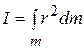 ; ; 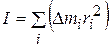
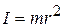 (для материальной точки) (для материальной точки)
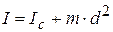 – теорема Штейнера – теорема Штейнера
|
| Второй закон Ньютона | 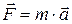
| 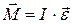
|
| Импульс; момент импульса | 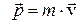
| 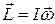 ; ; 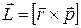
|
| Второй закон Ньютона в импульсной форме | 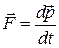
| 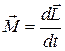
|
| Закон сохранения импульса; момента импульса | 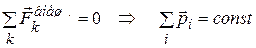
| 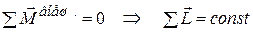 
|
| Работа | 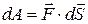
| 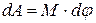
|
| Кинетическая энергия | 
| 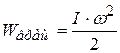
|
Колебания и волны
 1. Колебательные процессы. Гармонические колебания. Понятие о спектральном разложении
1. Колебательные процессы. Гармонические колебания. Понятие о спектральном разложении
Любой процесс, повторяющийся во времени, является колебательным. Физическая природа колебаний может быть различна: может изменяться координата (механические колебания), сила тока, напряжённость электрического или магнитного поля (электромагнитные колебания) и т.д., но физически различные процессы описываются одинаковыми уравнениями.
Рассмотрим гармонические колебания, то есть колебания, происходящие по гармоническому закону ( 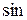 или
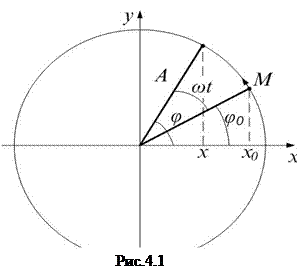
или 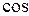 ). Представим себе материальную точку М, равномерно вращающуюся по окружности радиуса А с угловой скоростью ω (рис.4.1). Тогда проекция точки М на ось х будет совершать периодические колебания вдоль оси OX:
). Представим себе материальную точку М, равномерно вращающуюся по окружности радиуса А с угловой скоростью ω (рис.4.1). Тогда проекция точки М на ось х будет совершать периодические колебания вдоль оси OX:
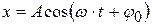 , (4.1)
, (4.1)
где А – амплитуда колебаний (абсолютное значение максимального смещения), 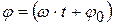 – фаза колебаний, которая определяет угловое смещение точки М в любой момент времени,
– фаза колебаний, которая определяет угловое смещение точки М в любой момент времени,  – начальная фаза,
– начальная фаза, 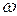 – круговая (циклическая) частота, равная
– круговая (циклическая) частота, равная
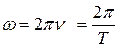 ; (4.2)
; (4.2)
ν – частота колебаний (число полных колебаний в единицу времени, 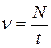 ,
, 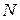 – число колебаний за время t),
– число колебаний за время t), 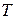 – период колебаний (время совершения одного полного колебания). Выражение (4.1) – кинематическое уравнение гармонического колебательного движения.
– период колебаний (время совершения одного полного колебания). Выражение (4.1) – кинематическое уравнение гармонического колебательного движения.
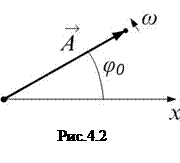 Можно представить гармонические колебания графически – это метод векторных диаграмм. Вращение вектора
Можно представить гармонические колебания графически – это метод векторных диаграмм. Вращение вектора 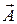 на рис.4.2 эквивалентно гармоническому колебанию.
на рис.4.2 эквивалентно гармоническому колебанию.
Ещё одно возможное представление гармонических колебаний – представление в виде комплексного числа:
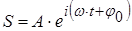 . (4.3)
. (4.3)
При этом не теряется информация о координате y точки М на рис.4.1, поскольку из (4.3) по формуле Эйлера получим:
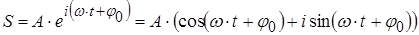 ,
,
или
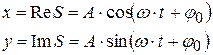
Ещё одно преимущество записи колебания (4.3): физические задачи на колебания сводятся просто к операциям с комплексными числами.
Почему рассматриваем в первую очередь именно гармонические колебания? Ведь реальные процессы чаще описываются негармоническими функциями. По теореме Фурье любую периодическую функцию 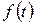 с периодом
с периодом 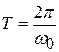 (
( 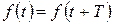 ) можно представить в виде ряда (ряд Фурье):
) можно представить в виде ряда (ряд Фурье):
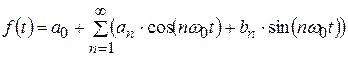 , (4.4)
, (4.4)
где
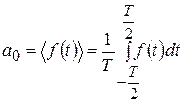 – среднее значение функции
– среднее значение функции 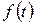 ;
;
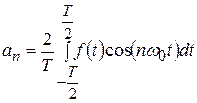 ;
; 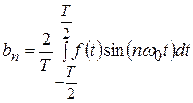 .
.
Иными словами, любое периодическое колебание можно представить в виде суперпозиции гармонических колебаний кратных частот 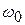 ,
, 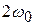 ,
, 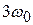 , …. Частота
, …. Частота 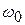 называется основной частотой;
называется основной частотой; 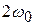 – первый обертон и т.д.
– первый обертон и т.д.
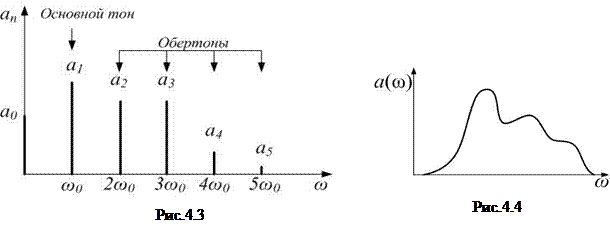
Определение: совокупность частот и соответствующих им амплитуд называется спектром колебания. Спектр можно представить графически. Пусть 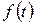 – чётная:
– чётная:
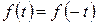
тогда все 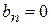 :
: 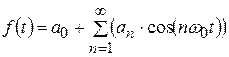 , и спектр состоит только из чётных гармоник (рис.4.3).
, и спектр состоит только из чётных гармоник (рис.4.3).
Реально можно ограничиться первыми несколькими членами ряда, если функция не очень «плохая».
Периодическая функция имеет дискретный спектр. Непериодическую тоже можно разложить по гармоническим составляющим, но это она будет иметь непрерывный спектр 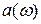 (рис.4.4), а ряд Фурье переходит в интеграл Фурье.
(рис.4.4), а ряд Фурье переходит в интеграл Фурье.
Дата добавления: 2015-04-10; просмотров: 1324;
