С. Сложение взаимно перпендикулярных колебаний кратных частот. Фигуры Лиссажу
Складываются колебания:
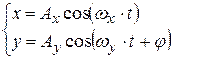
Решение задачи в общем случае очень сложное, поэтому ограничимся примерами. Если частоты относятся как небольшие целые числа:
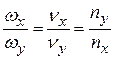 , (4.22)
, (4.22)
то фигура замкнута; условие замкнутости: 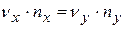 .
.
В методе фигур Лиссажу соотношение (4.22) по форме фигуры позволит найти незвестную частоту, если вторая частота известна. Здесь 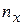 и
и 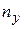 – число точек пересечения фогуры с осями OX и OY (или прямыми, параллельными этим осям) – см. рис.4.11.
– число точек пересечения фогуры с осями OX и OY (или прямыми, параллельными этим осям) – см. рис.4.11.
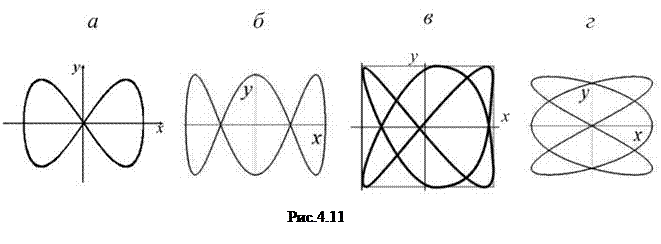 а)
а) 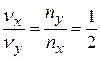 ; б)
; б) 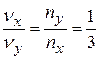 ; в)
; в) 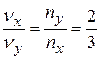 ; г)
; г) 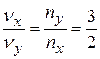 .
.
Дата добавления: 2015-04-10; просмотров: 2139;
